题目内容
7.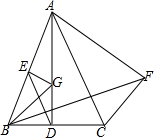 如图,△ABC中,AB=AC,D,E分别是BC,AB的中点,作BF⊥AC且使BF=AC,BG平分∠ABF.
如图,△ABC中,AB=AC,D,E分别是BC,AB的中点,作BF⊥AC且使BF=AC,BG平分∠ABF.(1)判断△BDG的形状,并证明你的结论;
(2)求证:△DGE∽△BCF.
分析 (1)根据直角三角形的性质,可得∠FBA+∠BAC=90°,根据等式的性质,可得∠GBF+∠CBF=$\frac{1}{2}$(∠BAC+∠ABF)=45°,根据等腰直角三角形的判定,可得答案;
(2)根据等腰三角形的性质,可得∠EDA=∠EAD=∠CBF,根据等量代换,可得BG=BD=$\frac{1}{2}$BC,ED=$\frac{1}{2}$AB=$\frac{1}{2}$AC=$\frac{1}{2}$BF,根据相似三角形的判定,可得答案.
解答 解:(1)△BDG是等腰直角三角形,
证明:∵BF⊥AC,
∴∠FBA+∠BAC=90°.
∵AB=AC,BD=DC,
∠DAC=$\frac{1}{2}$∠BAC,∠DAC=DBF.
∵∠GBF=$\frac{1}{2}$∠ABF,
∴∠GBF+∠CBF=$\frac{1}{2}$(∠BAC+∠ABF)=45°,
∴∠BGD=45°,
∴∠DBG=∠BGD,
∴DB=DG,
∴△BDG是等腰直角三角形;
(2)∵EA=EB=ED,
∴∠EDA=∠EAD=∠CBF.
∵BG=BD=$\frac{1}{2}$BC,ED=$\frac{1}{2}$AB=$\frac{1}{2}$AC=$\frac{1}{2}$BF,
∴$\frac{GD}{BC}$=$\frac{ED}{BF}$=$\frac{1}{2}$,
∴△DGE∽△BCF
点评 本题考查了相似三角形的判定,(1)利用了直角三角形的性质,等腰三角形的性质,等式的性质,等腰直角三角形的判定;(2)利用了等腰三角形的性质,等量代换,利用等量代换得出BG=BD=$\frac{1}{2}$BC,ED=$\frac{1}{2}$AB=$\frac{1}{2}$AC=$\frac{1}{2}$BF是解题关键.

| A. | 2006 | B. | 1-20072 | C. | 1-20062 | D. | 123456 |
| A. | 5 | B. | 6 | C. | 7 | D. | 13 |
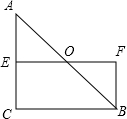 如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC,求证:四边形BCEF是矩形.
如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC,求证:四边形BCEF是矩形.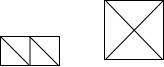 如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.
如图,将两个边长为$\sqrt{3}$的正方形对角线剪开,将所得的四个三角形拼成一个大的正方形,则这个大正方形的边长是$\sqrt{6}$.