题目内容
19.已知一次函数的图象经过点P(0,2),且与两坐标轴截得的直角三角形的面积为4,求一次函数的解析式,并画出图象.分析 在直角三角形中,已知一边OP=2,根据三角形的面积即可求得另一直角边的长度,即与x轴交点的横坐标,求出与x轴的交点坐标,利用待定系数法即可求得一次函数的解析式.
解答 解:①当一次函数与x轴交点Q在x轴负半轴时,
由OP=2,与两坐标所围成的直角三角形面积为4,得到Q(-4,0),
设一次函数解析式为y=kx+b,
将P与Q坐标代入得:$\left\{\begin{array}{l}{b=2}\\{-4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
此时一次函数解析式为y=$\frac{1}{2}$x+2;
②当一次函数与x轴交点在x轴正半轴时,
由OP=2,与两坐标所围成的直角三角形面积为4,得到Q(4,0),
设一次函数解析式为y=mx+n,
将P与Q坐标代入得:$\left\{\begin{array}{l}{n=2}\\{4m+n=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=2}\end{array}\right.$,
此时一次函数解析式为y=-$\frac{1}{2}$x+2;
综上,一次函数解析式为:y=$\frac{1}{2}$x+2或y=-$\frac{1}{2}$x+2.
函数图象如图: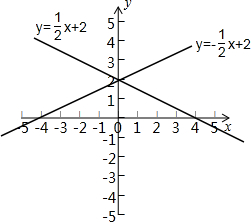
点评 本题主要考查待定系数法求函数解析式,是常用的求解析式的方法,注意到分两种情况讨论是解决本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.如果a>b,那么下列结论一定正确的是( )
| A. | a-3<b-3 | B. | -4a>-4b | C. | 3-a>3-b | D. | $-\frac{a}{3}<-\frac{b}{3}$ |
14.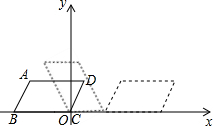 已知,平行四边形ABCD在直角坐标系内的位置如图所示,且AB=2,BC=3,∠ABC=60°,点C在原点,把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转,经过505次翻转后,点A的坐标是( )
已知,平行四边形ABCD在直角坐标系内的位置如图所示,且AB=2,BC=3,∠ABC=60°,点C在原点,把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转,经过505次翻转后,点A的坐标是( )
 已知,平行四边形ABCD在直角坐标系内的位置如图所示,且AB=2,BC=3,∠ABC=60°,点C在原点,把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转,经过505次翻转后,点A的坐标是( )
已知,平行四边形ABCD在直角坐标系内的位置如图所示,且AB=2,BC=3,∠ABC=60°,点C在原点,把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转,经过505次翻转后,点A的坐标是( )| A. | ($\frac{2525}{2}$,$\sqrt{3}$) | B. | ($\frac{2521}{2}$,$\frac{3}{2}$$\sqrt{3}$) | C. | (1008,$\sqrt{3}$) | D. | (1008,$\frac{3}{2}$$\sqrt{3}$) |
4.现在互联网越来越普及,网上购物的人也越来越多,订购的商品往往通过快递送达.淘宝网上某“四皇冠”级店铺率先与“快乐童年”童装厂取得联系,经营该厂家某种型号的童装.根据第一周的销售记录,该型号童装每天的售价x(元/件)与当日的销售量y(件)的相关数据如下表:
已知该型号童装每件的进价是70元,同时为吸引顾客,该店铺承诺,每件服装的快递费10元由卖家承担.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求第一周销售中,y与x的函数关系式;
(2)设第一周每天的赢利为w元,求w关于x的函数关系式,并求出每天的售价为多少元时,每天的赢利最大?最大赢利是多少?
(3)从第二周起,该店铺一直按第(2)中的最大日盈利的售价进行销售.但进入第三周后,网上其他购物店也陆续推出该型号童装,因此第三、四周该店铺每天的售价都比第二周下降了m%,销售量也比第二周下降了0.5m%(m<20);第五周开始,厂家给予该店铺优惠,每件的进价降低了16元;该店铺在维持第三、四周的销售价和销售量的基础上,同时决定每件童装的快递费由买家自付,这样,第五周的赢利相比第二周的赢利增加了2%,请估算整数m的值.
| 每件的销售价x(元/件) | 200 | 190 | 180 | 170 | 160 | 150 | 140 |
| 每天的销售量y(件) | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求第一周销售中,y与x的函数关系式;
(2)设第一周每天的赢利为w元,求w关于x的函数关系式,并求出每天的售价为多少元时,每天的赢利最大?最大赢利是多少?
(3)从第二周起,该店铺一直按第(2)中的最大日盈利的售价进行销售.但进入第三周后,网上其他购物店也陆续推出该型号童装,因此第三、四周该店铺每天的售价都比第二周下降了m%,销售量也比第二周下降了0.5m%(m<20);第五周开始,厂家给予该店铺优惠,每件的进价降低了16元;该店铺在维持第三、四周的销售价和销售量的基础上,同时决定每件童装的快递费由买家自付,这样,第五周的赢利相比第二周的赢利增加了2%,请估算整数m的值.
8.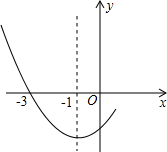 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
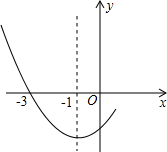 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )| A. | ①② | B. | ②③ | C. | ①②④ | D. | ②③④ |
9.下列四个实数中,最小的是( )
| A. | -3 | B. | -π | C. | -$\sqrt{5}$ | D. | 0 |