题目内容
11.①用适当的方法解方程:2(x-3)2=3(3-x)②二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),试求这个二次函数的解析式.
分析 ①先移项,再提取公因式,把原式化为两个因式积的形式即可得出结论;
②把A(m,4)代入反比例函数y=-$\frac{8}{x}$求出m的值,故可得出A点坐标,再把A、B两点坐标代入二次函数y=x2+bx+c,求出b、c的值即可.
解答 解:①移项得,2(x-3)2-3(3-x)=0,
提取公因式得,(x-3)(2x-6+3)=0,即(x-3)(2x-3)=0,解得x1=3,x2=$\frac{3}{2}$;
②∵反比例函数y=-$\frac{8}{x}$的图象过点A(m,4),
∴-$\frac{8}{m}$=4,解得m=-2,
∴A(-2,4).
∵二次函数y=x2+bx+c的图象过点B(0,-2),A(-2,4),
∴$\left\{\begin{array}{l}c=-2\\ 4-2b+c=4\end{array}\right.$,解得$\left\{\begin{array}{l}c=-2\\ b=-1\end{array}\right.$,
∴二次函数的解析式为y=x2-x-2.
点评 本题考查的是待定系数法求二次函数的解析式,熟知二次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数y=x+3与y=$-\frac{2}{x}$的图象的交点为(a,b),则$\frac{1}{a}-\frac{1}{b}$的值是( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
 如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点.
如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点.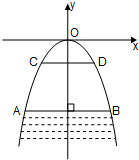 有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.
有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离. 如图,正方形ABCD,点M在CD上,在AC上确定点N,使DN+MN最小.
如图,正方形ABCD,点M在CD上,在AC上确定点N,使DN+MN最小.