题目内容
14.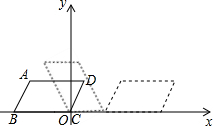 已知,平行四边形ABCD在直角坐标系内的位置如图所示,且AB=2,BC=3,∠ABC=60°,点C在原点,把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转,经过505次翻转后,点A的坐标是( )
已知,平行四边形ABCD在直角坐标系内的位置如图所示,且AB=2,BC=3,∠ABC=60°,点C在原点,把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转,经过505次翻转后,点A的坐标是( )| A. | ($\frac{2525}{2}$,$\sqrt{3}$) | B. | ($\frac{2521}{2}$,$\frac{3}{2}$$\sqrt{3}$) | C. | (1008,$\sqrt{3}$) | D. | (1008,$\frac{3}{2}$$\sqrt{3}$) |
分析 作A1M⊥x轴于M,则DM=$\frac{1}{2}$AD=$\frac{3}{2}$,得出OM=CD-DM=$\frac{1}{2}$,A1M=$\frac{3\sqrt{3}}{2}$,得出A1的坐标为($\frac{1}{2}$,$\frac{3\sqrt{3}}{2}$),画出第3次、第4次翻转后的图形,容易发现规律:每翻转4次,图形向右平移10.点A1向右平移126×10(即1260)到点A505.即可得出结果.
解答 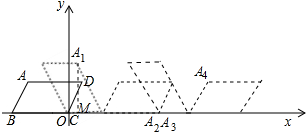 解:作A1M⊥x轴于M,如图所示:
解:作A1M⊥x轴于M,如图所示:
则DM=$\frac{1}{2}$AD=$\frac{3}{2}$,
∴OM=CD-DM=$\frac{1}{2}$,
∴A1M=$\frac{3\sqrt{3}}{2}$,
∴A1的坐标为($\frac{1}{2}$,$\frac{3\sqrt{3}}{2}$),
画出第3次、第4次翻转后的图形,如图所示:
由图可知:每翻转4次,图形向右平移10.
∵505=126×4+1,
∴点A1向右平移126×10(即1260)到点A505.
∵A1的坐标为($\frac{1}{2}$,$\frac{3\sqrt{3}}{2}$),
∴经过505次翻转后,点A的坐标是(1260+$\frac{1}{2}$,$\frac{3\sqrt{3}}{2}$),
即($\frac{2521}{2}$,$\frac{3\sqrt{3}}{2}$).
故选:B.
点评 本题考查了平行四边形的性质、三角函数、考查了操作、探究、发现规律的能力.发现“每翻转4次,图形向右平移10”是解决本题的关键.

练习册系列答案
相关题目
9.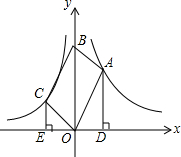 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
 在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
在平面直角坐标系xOy中,函数y=$\frac{{k}_{1}}{x}$(k1>0,x>0)、函数y=$\frac{{k}_{2}}{x}$(k2<0,x<0)的图象分别经过?OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )| A. | 4:9 | B. | 2:3 | C. | 3:2 | D. | 9:4 |
3.函数y=x+3与y=$-\frac{2}{x}$的图象的交点为(a,b),则$\frac{1}{a}-\frac{1}{b}$的值是( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
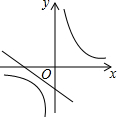
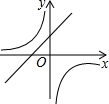
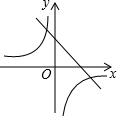
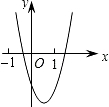 二次函数y=ax2+bx+c的图形如图所示,则一次函数y=ax-c与反比例函数y=$\frac{a+b+c}{x}$在同一坐标系内的图象大致为( )
二次函数y=ax2+bx+c的图形如图所示,则一次函数y=ax-c与反比例函数y=$\frac{a+b+c}{x}$在同一坐标系内的图象大致为( )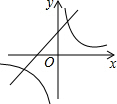
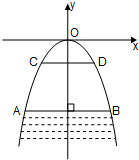 有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.
有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离. 如图,⊙O的半径是2,∠ACB=30°,则小扇形AOB的面积是$\frac{2}{3}$π(结果保留π).
如图,⊙O的半径是2,∠ACB=30°,则小扇形AOB的面积是$\frac{2}{3}$π(结果保留π).