题目内容
8.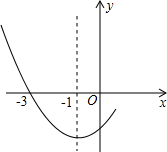 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )| A. | ①② | B. | ②③ | C. | ①②④ | D. | ②③④ |
分析 根据函数的开口方向可以确定a的正负,根据顶点坐标所在的位置可以确定b与a的关系,根据函数图象与y轴的交点可以确定c的正负,从而可以判断①是否正确;
根据对称轴的公式和对称轴为x=-1,可以判断2a-b的正负,从而可以判断②;
根据二次函数具有对称性,可以判③是否正确;
根据函数图象可以判断④是否正确.
解答 解:由图象可知,抛物线开口向上,则a>0,
顶点在y轴左侧,则b>0,
抛物线与y轴交于负半轴,则c<0,
∴abc<0,故①正确;
∵对称轴为x=-1,对称轴x=-$\frac{b}{2a}$,
∴-$\frac{b}{2a}$=-1,
可得2a-b=0,故②正确;
由图象可知,当x=2时的函数值与x=-3时的函数值相等,故4a+2b+c=0,故③错误;
由图象可知,x=-5时的函数值大于0,x=0时的函数值小于0,故y1>y2,故④正确;
故选C.
点评 本题考查二次函数图象与系数的关系,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
3.函数y=x+3与y=$-\frac{2}{x}$的图象的交点为(a,b),则$\frac{1}{a}-\frac{1}{b}$的值是( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
18.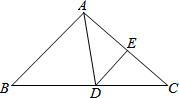 如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )
如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )
 如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )
如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是( )| A. | 24cm | B. | 26cm | C. | 28cm | D. | 30cm |
 如图,正方形ABCD,点M在CD上,在AC上确定点N,使DN+MN最小.
如图,正方形ABCD,点M在CD上,在AC上确定点N,使DN+MN最小.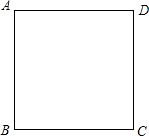 正方形、等边三角形是常见的轴对称图形.如图,设有一个边长为1的正方形ABCD,试在这个正方形中找出一个面积最大的和一个面积最小的内接等边三角形,并求出这两个图形的面积.
正方形、等边三角形是常见的轴对称图形.如图,设有一个边长为1的正方形ABCD,试在这个正方形中找出一个面积最大的和一个面积最小的内接等边三角形,并求出这两个图形的面积.