题目内容
6.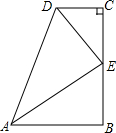 在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
分析 过点E作EF⊥AD,垂足为F.由三角形的内角和定理求得∠CDE=55°,由角平分线的定义可知∠CDA=110°,由平行线的判定定理可知AB∥CD,由平行线的性质可求得∠DAB=70°,由角平分线的性质可知EF=EC,于是得到EF=BE,根据HL可证明Rt△AEF≌Rt△AEB,从而得到∠EAB=$\frac{1}{2}∠$DAB=35°.
解答 解:过点E作EF⊥AD,垂足为F.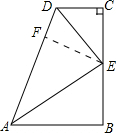
∵∠C=90°,∠CED=35°,
∴∠CDE=55°.
∵DE平分∠ADC,
∴∠EDF=55°.
∴∠CDA=110°.
∵∠B=∠C=90°,
∴AB∥CD.
∴∠CDA+∠DAB=180°.
∴∠DAB=70°.
∵DE平分∠CDA,EF⊥AD,EC⊥DC,
∴EF=EC.
∵E是BC的中点,
∴EF=BE.
在Rt△AEF和Rt△AEB中,$\left\{\begin{array}{l}{EF=BE}\\{AE=AE}\end{array}\right.$,
∴Rt△AEF≌Rt△AEB.
∴∠EAF=∠EAB.
∴∠EAB=$\frac{1}{2}∠$DAB=$\frac{1}{2}×70°$=35°.
故选:D.
点评 本题主要考查的是角平分线的性质、全等三角形的性质和判定、平行线的性质和判定、三角形的内角和定理,由角平分线的性质证得EF=EC是解题的关键.

练习册系列答案
相关题目
1.长春市2014年城市道路改建总投资达到209亿元,用科学记数法表示209亿元应为( )
| A. | 209×108元 | B. | 209×109元 | C. | 2.09×1010元 | D. | 2.09×1011元 |
 如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.
如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.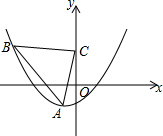 已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标.
已知,抛物线y=$\frac{1}{8}$(x+1)2-2顶点为A,点B在抛物线上,以AB的斜边作等腰直角三角形,直角顶点C在y轴上,求C点坐标. 已知:AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:
已知:AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证: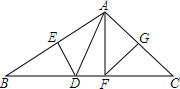 如图,在△ABC中,DE、FG分别为AB、AC的垂直平分线,连接AD、AF.
如图,在△ABC中,DE、FG分别为AB、AC的垂直平分线,连接AD、AF.