题目内容
20. 如图,在△ABC中,在BC上取点D,使CD=AB,点E在AC上,连接AD、DE,且AD=DE,∠BAD=∠CDE.
如图,在△ABC中,在BC上取点D,使CD=AB,点E在AC上,连接AD、DE,且AD=DE,∠BAD=∠CDE.(1)求证:∠B=∠C;
(2)若∠DAE=∠DEA=∠B+30°,求∠ADB的度数.
分析 (1)根据两边和它们的夹角分别相等的两个三角形全等,可得答案;
(2)根据全等三角形的性质,可得∠ADB=∠DEC,根据三角形的内角和、邻补角,可得二元一次方程组,根据解方程组,可得答案.
解答 解:(1)在△ABD和△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAD=∠CDE}\\{AD=DE}\end{array}\right.$,
∴△ABD≌△DCE(SAS),
∠B=∠C;
(2)在△ABD和△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAD=∠CDE}\\{AD=DE}\end{array}\right.$,
∴△ABD≌△DCE(SAS),
∴∠ADB=∠DEC.
∴∠ADC=∠DEA
∵∠DAE=∠DEA=30°+∠B,
∴∠ADC=∠DEA=∠DAE=30°+∠B,
∴∠BAD=∠CDE=30°,
设∠ADC=∠DEA=∠DAE=y,∠ADB=∠DEC=x.得:
$\left\{\begin{array}{l}{180-2y+30=y①}\\{x+y=180②}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=110}\\{y=70}\end{array}\right.$.°
∴∠ADB=110°
点评 本题考查了全等三角形的判定与性质,根据条件选择相应的判定方法是解题关键;利用三角形的内角和、邻补角得出不等式组是解题关键.

练习册系列答案
相关题目
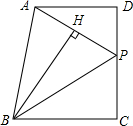 如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
 如图,在△ABC中,AB=AC,AD是中线,CE∥AD交BA的延长线于点E,请判断△AEC的形状,并说明理由.
如图,在△ABC中,AB=AC,AD是中线,CE∥AD交BA的延长线于点E,请判断△AEC的形状,并说明理由. 如图,在△ABC中,D,E,F,G分别是AC,AB,ED,BF的五等分点、四等分点、三等分点,二等分点,若△ABC的面积是25,则△FGD的面积是5.
如图,在△ABC中,D,E,F,G分别是AC,AB,ED,BF的五等分点、四等分点、三等分点,二等分点,若△ABC的面积是25,则△FGD的面积是5. 已知:如图,锐角△ABC的两条高BE,CD相交于点O,且BE=CD.
已知:如图,锐角△ABC的两条高BE,CD相交于点O,且BE=CD. 已知y关于x的一次函数y=(2m2-32)x3-(n-3)x2+(m-n)x+m+n.
已知y关于x的一次函数y=(2m2-32)x3-(n-3)x2+(m-n)x+m+n.