题目内容
7. 如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的
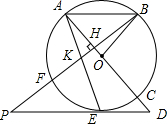
如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的延长线交⊙O于点E,过点E作PD∥AB,PD与AC、BF的延长线分别交于点D、P.
(1)求证:PD是⊙O的切线;
(2)若AK=$\sqrt{10}$,tan∠BAH=$\frac{4}{3}$,求⊙O半径的长.
分析 (1)连接OE,根据等腰三角形的性质得出∠OEA=∠OAE,∠AKB=∠BAE,然后根据平行线的性质∠PEA=∠AKB,进而即可证得∠OEA+∠PEA=90°,即OE⊥PD,即可证得结论;
(2)根据已知设AH=3n,则BH=4n,AB=5n,KH=n,然后根据勾股定理列出关于n的方程,解得n=1,得出AH=3,BH=4,设⊙O半径为R,则在Rt△OBH中,OH=R-3,根据勾股定理得出关于R的方程,解方程即可求得.
解答 解:(1)连接OE,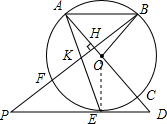
∵OE=OA,
∴∠OEA=∠OAE,
∵PD∥AB,
∴∠PEA=∠BAE,
∵KB=AB,
∴∠AKB=∠BAE,
∴∠PEA=∠AKB,
∵BF⊥AC,H为垂足,
∴∠OAE+∠AKB=90°
∴∠OEA+∠PEA=90°,
即OE⊥PD,
∴PD是⊙O的切线;
(2)解:∵tan∠BAH=$\frac{4}{3}$,BF⊥AC,H为垂足,且KB=AB,
在Rt△ABH和Rt△AKH中,设AH=3n,则BH=4n,AB=5n,KH=n,
∴由AH2+KH2=AK2,即(3n)2+n2=($\sqrt{10}$)2,解得n=1,
∴AH=3,BH=4,
设⊙O半径为R,则在Rt△OBH中,OH=R-3,
由OH2+BH2=OB2,即(R-3)2+42=R2,解得:R=$\frac{25}{6}$,
∴⊙O半径的长为$\frac{25}{6}$.
点评 本题考查的是圆的综合题,涉及到切线的判定,平行线性质,等腰三角形的性质以及勾股定理的应用,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.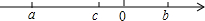 已知,三个实数a,b,c在数轴上的点如图所示,|a-b|+|c-a|-|c+b|的值可能是( )
已知,三个实数a,b,c在数轴上的点如图所示,|a-b|+|c-a|-|c+b|的值可能是( )
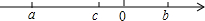 已知,三个实数a,b,c在数轴上的点如图所示,|a-b|+|c-a|-|c+b|的值可能是( )
已知,三个实数a,b,c在数轴上的点如图所示,|a-b|+|c-a|-|c+b|的值可能是( )| A. | 2a | B. | 2b | C. | 2c | D. | -2a |
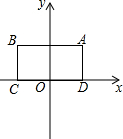 对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为($\sqrt{3}$,2),顶点C、D在x轴上,且OC=OD.
对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为($\sqrt{3}$,2),顶点C、D在x轴上,且OC=OD.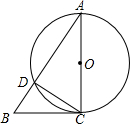 如图,AC是⊙O的直径,∠A=30°,AB交⊙O于D,CD=1,
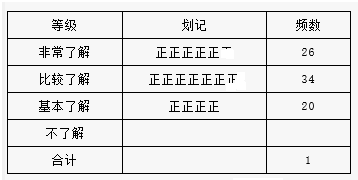
如图,AC是⊙O的直径,∠A=30°,AB交⊙O于D,CD=1,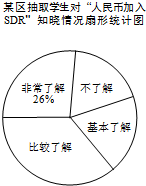 “世界那么大,我想去看看”一句话红遍网络,随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR(特别提款权),以后出国看世界更加方便.为了解某区6000名初中生对“人民币加入SDR”知晓的情况,某校数学兴趣小组随机抽取区内部分初中生进行问卷调查,将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级,并将调查结果整理分析,得到下列图表:
“世界那么大,我想去看看”一句话红遍网络,随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR(特别提款权),以后出国看世界更加方便.为了解某区6000名初中生对“人民币加入SDR”知晓的情况,某校数学兴趣小组随机抽取区内部分初中生进行问卷调查,将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级,并将调查结果整理分析,得到下列图表: