题目内容
15.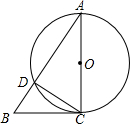 如图,AC是⊙O的直径,∠A=30°,AB交⊙O于D,CD=1,
如图,AC是⊙O的直径,∠A=30°,AB交⊙O于D,CD=1,(1)求AC的长;
(2)若BC=$\frac{2\sqrt{3}}{3}$,求证:BC是⊙O的切线.
分析 (1)直接利用圆周角定理得出∠ADC=90°,再利用直角三角形的性质得出AC=2CD,进而得出答案;
(2)利用锐角三角函数关系得出∠B的度数,再利用切线的判定方法得出答案.
解答 (1)解:∵AC是⊙O的直径,
∴∠ADC=90°,
又∵∠A=30°,CD=1,
∴AC=2CD=2;
(2)证明:由(1)知,在直角△BCD中,
∵BC=$\frac{2\sqrt{3}}{3}$,CD=1,
∴sinB=$\frac{CD}{BC}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠B=60°,
∴∠A+∠B=90°,
∴∠ACB=90°,
∴BC是⊙O 的切线.
点评 此题主要考查了切线的判定以及锐角三角函数关系,正确得出∠B的度数是解题关键.

练习册系列答案
相关题目
10.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.25;(精确到0.01)
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
| 摸到白球的频率$\frac{m}{n}$ | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
5.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是( )
| A. | (-4,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
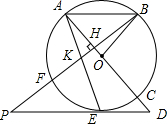 如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的
如图,AC是⊙O的直径,BF是⊙O的弦,BF⊥AC于点H,在BF上截取KB=AB,AK的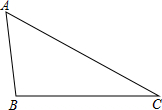 如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:
如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题: