题目内容
2．（1）计算：（-2）2+（$\frac{1}{2}$）-1+$\root{3}{-8}$-$\sqrt{9}$（2）解方程：$\frac{1-x}{x-2}$+2=$\frac{1}{2-x}$．
分析 （1）原式第一项利用乘方的意义计算，第二项利用负整数指数幂法则计算，第三项利用立方根定义计算，最后一项利用算术平方根定义计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=4+2-2-3=1；
（2）去分母得：1-x+2x-4=-1，
解得：x=2，
经检验x=2是增根，分式方程无解．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
10．在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．表是活动进行中的一组统计数据：
（1）请估计：当n很大时，摸到白球的频率将会接近0.25；（精确到0.01）
（2）试估算口袋中白种颜色的球有多少只？
（3）请根据估算的结果思考从口袋中先摸出一球，不放回，再摸出一球；这两只球颜色不同的概率是多少？画出树状图（或列表）表示所有可能的结果，并计算概率．
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
| 摸到白球的频率$\frac{m}{n}$ | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
（2）试估算口袋中白种颜色的球有多少只？
（3）请根据估算的结果思考从口袋中先摸出一球，不放回，再摸出一球；这两只球颜色不同的概率是多少？画出树状图（或列表）表示所有可能的结果，并计算概率．
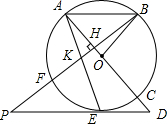如图，AC是⊙O的直径，BF是⊙O的弦，BF⊥AC于点H，在BF上截取KB=AB，AK的
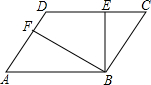如图，在?ABCD中，BE⊥CD，BF⊥AD，垂足分别为E，F，CE=2，DF=1，∠EBF=60°，则?ABCD的周长为20．
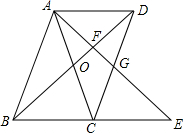如图，?ABCD中，AC与BD相交于点O，AB=AC，延长BC到点E，使CE=BC，连接AE，分别交BD、CD于点F、G．