题目内容
4.计算:1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{10}}$.分析 根据题目中的式子的特点,可以求得题目中式子的结果.
解答 解:设S=1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{10}}$,
则$\frac{1}{3}$S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{10}}$+$\frac{1}{{3}^{11}}$,
∴S-$\frac{1}{3}S$=1-$\frac{1}{{3}^{11}}$,
解得,S=$\frac{3}{2}-\frac{1}{2×{3}^{10}}$,
即$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{10}}$=$\frac{3}{2}-\frac{1}{2×{3}^{10}}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.

练习册系列答案
相关题目
9.已知A32=3×2=6,A52=5×4=20,A63=6×5×4=120,依此规律A74=( )
| A. | 480 | B. | 360 | C. | 840 | D. | 1080 |
 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,找出图中相等的角,并说明理由.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,找出图中相等的角,并说明理由.
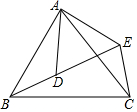 如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.
如图,在四边形ABCE中,点D在对角线BE上,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ABD=∠ACE.