Question

14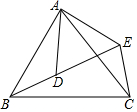．如图，在四边形ABCE中，点D在对角线BE上，$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$，求证：∠ABD=∠ACE．

Answer 1

分析 由$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$，可证得△ABC∽△ADE，即可得∠BAD=∠CAE，然后由有两边对应成比例且夹角相等三角形相似，证得△ABD∽△ACE，继而证得结论．

解答 证明：∵$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$，
∴△ABC∽△ADE，AB：AC=AD：AE，
∴∠BAC=∠DAE，
∴∠BAD=∠CAE，
∴△ABD∽△ACE，
∴∠ABD=∠ACE．

点评 此题考查了相似三角形的判定与性质．注意证得△ABD∽△ACE是解此题的关键．