题目内容
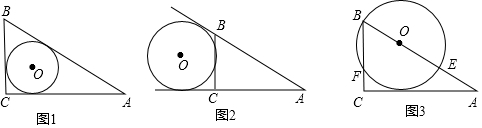
14.如图1,在Rt△ABC中,∠C=90°,AB、BC、AC的长分别是c、a、b,根据“切线长定理”,我们易证得△ABC的内切圆半径r=$\frac{a+b-c}{2}$,当⊙O符合下列条件时,求半径r.(1)如图2,圆心O在直角三角形外,且⊙O与三角形三边均相切;
(2)如图3,圆心O在直角三角形斜边上,且⊙O与其中一条直角边相切.
分析 (1)如图2,设⊙O与△ABC的边或边的延长线的三个切点分别是D、E、F,连接OE,OF,易得四边形CFOE是正方形,然后利用切线长定理,即可求得答案;
(2)如图3,设⊙O与直角边AC的切点为D,连接OD,易证得OD∥BC,根据平行线分线段成比例定理,即可求得答案.
解答 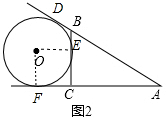 解:如图2,设⊙O与△ABC的边或边的延长线的三个切点分别是D、E、F,连接OE,OF,
解:如图2,设⊙O与△ABC的边或边的延长线的三个切点分别是D、E、F,连接OE,OF,
∴OE⊥BC,OF⊥AC,
∴∠OEC=∠OFC=90°,
∵∠ACB=90°,
∴四边形CFOE是矩形,
∵OF=OE,
∴四边形CFOE是正方形,
∴OF=OE=CE=CF=r,
BD=BE=BC-CE=a-r,
由切线长定理得,
∵AD=AF,
即b+r=c+(a-r),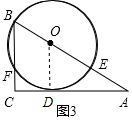
∴r=$\frac{c+a-b}{2}$;
(2)如图3,设⊙O与直角边AC的切点为D,连接OD,
∴OD⊥AC,
∴OD∥BC,
∴$\frac{OD}{BC}=\frac{OA}{AB}$即$\frac{r}{a}=\frac{c-r}{c}$,
∴r=$\frac{ac}{a+c}$.
点评 此题考查了内切圆的性质、正方形的判定与性质,平行线的判定与性质以及直角三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.化简($\frac{1}{x-3}$-$\frac{x+1}{{x}^{2}-1}$)•(x-3)的结果是( )
| A. | 2 | B. | $\frac{x-4}{x-1}$ | C. | $\frac{2}{x-3}$ | D. | $\frac{2}{x-1}$ |
5.下列命题中,真命题是( )
| A. | 两对角线相等的四边形是矩形 | |
| B. | 两对角线互相平分的四边形是平行四边形 | |
| C. | 两对角线互相垂直的四边形是菱形 | |
| D. | 两对角线互相垂直且平分的四边形是正方形 |
 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE. 如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′.
如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′. 抛物线y=-x2+2x+n经过点M(-1,0),顶点为C.
抛物线y=-x2+2x+n经过点M(-1,0),顶点为C. 如图,已知点D在锐角三角形ABC的BC边上,AB>AC,点E、F分别是△ABD、△ACD的外心,且EF=BC,那么∠ADC=30度.
如图,已知点D在锐角三角形ABC的BC边上,AB>AC,点E、F分别是△ABD、△ACD的外心,且EF=BC,那么∠ADC=30度. 如图,已知BA=BD,BC=BE,∠1=∠2,求证:AC=DE.
如图,已知BA=BD,BC=BE,∠1=∠2,求证:AC=DE.