题目内容
2. 如图,正方形ODBC中,OB=$\sqrt{2}$,OA=OB,则数轴上点A表示的数是-$\sqrt{2}$.
如图,正方形ODBC中,OB=$\sqrt{2}$,OA=OB,则数轴上点A表示的数是-$\sqrt{2}$.
分析 在直角三角形中根据勾股定理求得OB的值,即OA的值,进而求出数轴上点A表示的数.
解答 解:∵OB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴OA=OB=$\sqrt{2}$,
∵点A在数轴上原点的左边,
∴点A表示的数是-$\sqrt{2}$,
故答案为:-$\sqrt{2}$.
点评 本题考查了实数与数轴,勾股定理,解题时需注意根据点的位置确定数的符号.

练习册系列答案
相关题目
13.已知$\sqrt{{(1-2x)}^2}=2x-1$,则x的取值范围是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x<$\frac{1}{2}$ |
17.以下各组数为三角形的三条边长,其中不能构成直角三角形的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 1,1,2 | D. | 5,12,13 |
14.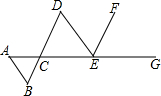 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )| A. | 0个 | B. | 1个 | C. | 3个 | D. | 5个 |
12.若∠α+∠β=180°,∠β+∠γ=180°,则∠α与∠γ的关系是( )
| A. | 互余 | B. | 互补 | C. | 相等 | D. | ∠α=90°+∠γ |
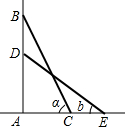 如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.
如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.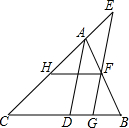 如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.
如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.