题目内容
12.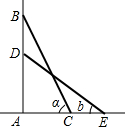 如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.
如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.(参考数据:sina=$\frac{4}{5}$,cosa=$\frac{3}{5}$,tana=$\frac{4}{3}$;sinb=$\frac{3}{5}$,cosb=$\frac{4}{5}$,tanb=$\frac{3}{4}$)
分析 设梯子的长度为x.通过解直角△ADE求得线段AD的长度;通过解直角△ABC得到线段AB的长度;然后结合AB-AD=1列出方程,通过解方程求得x的值.
解答 解:在直角△ADE中,∠DEA=b,DE=x,则AD=sinb•x=$\frac{3}{5}$x.
在直角△ABC中,∠ACB=a,BC=x,则AB=sina•x=$\frac{4}{5}$x.
依题意得:$\frac{4}{5}$x-$\frac{3}{5}$x=1,
解得x=5.
答:梯子的长度为5m.
点评 本题考查了解直角三角形的应用.主要是正弦概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
17.钓鱼岛是位于中国东海钓鱼岛列岛的主岛,自古以来都是中国的领土,其周围的海域面积约为170000平方公里,170000用科学记数法可表示为( )
| A. | 0.17×106 | B. | 1.7×105 | C. | 1.7×106 | D. | 17×104 |
 如图,正方形ODBC中,OB=$\sqrt{2}$,OA=OB,则数轴上点A表示的数是-$\sqrt{2}$.
如图,正方形ODBC中,OB=$\sqrt{2}$,OA=OB,则数轴上点A表示的数是-$\sqrt{2}$.