题目内容
5．已知样本x1，x2，x3，x4的平均数是$\overline x$，方差是S2，则样本x1+3，x2+3，x3+3，x4+3的平均数是$\overline{x}$+3；方差是s2．分析 根据平均数，方差的公式进行计算．
解答 解：平均数$\overline{x'}$=$\frac{1}{4}$（x1+3+x2+3+x3+3+x4+3）=$\overline{x}$+3，
方差s′2=$\frac{1}{4}$[（x1+3-$\overline{x}$-3）2+（x2+3-$\overline{x}$-3）2+…+（x4+3-$\overline{x}$-3）2]
=s2，
故答案为：$\overline{x}$+3，s2．
点评 本题考查了平均数、方差的计算．关键是熟悉计算公式，会将所求式子变形，再整体代入．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．下列式子一定是二次根式的是（ ）
| A． | $\sqrt{x+2}$ | B． | $\sqrt{x-2}$ | C． | $\sqrt{{x}^{2}+2}$ | D． | $\sqrt{{x}^{2}-2}$ |
20．下列运算中，正确的是（ ）
| A． | （x+2）2=x2+4 | B． | （-a+b）（a+b）=b2-a2 | C． | （x-2）（x+3）=x2-6 | D． | 3a3b2÷a2b2=3ab |
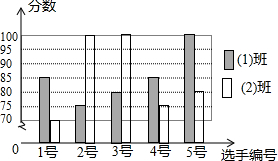为了弘扬“中国梦”，某校初三（1）班和初三（2）班各5名同学参加以“诚信•友善”为主题的演讲比赛活动，根据他们的得分情况绘制如下的统计图：