Question

20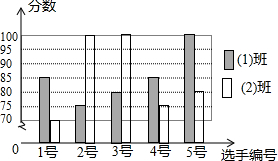．为了弘扬“中国梦”，某校初三（1）班和初三（2）班各5名同学参加以“诚信•友善”为主题的演讲比赛活动，根据他们的得分情况绘制如下的统计图：
（1）求初三（1）班5名参赛同学得分的平均数和初三（2）班5名参赛同学得分的众数．
（2）你认为哪个班5名同学参赛的整体成绩要好些？为什么？
（3）若该校初三有8个班级，每班参赛学生都是5名，根据这两个班的得分情况估计，初三参赛学生中得分超过90分的大约有多少人？

Answer 1

分析 （1）根据平均数与众数的定义分别求解即可；
（2）分别求出两个班的平均数与方差，再根据方差的意义求解即可；
（3）先求出初三（1）班与初三（2）班超过90分的学生人数，再利用样本估计总体的思想求解即可．

解答 解：（1）初三（1）班5名同学的成绩是85，75，80，85，100，
所以平均数是：（85+75+80+85+100）÷5=85；
初三（2）班5名同学的成绩是70，100，100，75，80，
100出现了2次，次数最多，所以众数是100；

（2）初三（2）班5名同学成绩的平均数是：（70+100+100+75+80）÷5=85，
初三（1）班5名同学成绩的方差是：$\frac{1}{5}$[（85-85）²+（75-85）²+（80-85）²+（85-85）²+（100-85）²]=70，
初三（2）班5名同学成绩的方差是：$\frac{1}{5}$[（70-85）²+（100-85）²+（100-85）²+（75-85）²+（80-85）²]=160，
两个班成绩的平均数都是85；而初三（1）班5名同学成绩的方差小于初三（2）班5名同学成绩的方差，
所以初三（1）班的整体成绩要好些；

（3）根据表格可知，初三（1）班有1名同学的成绩超过90分，初三（2）班有2名同学的成绩超过90分，
（1+2）×4=12，
所以初三参赛学生中得分超过90分的大约有12人．

点评 本题考查了平均数、众数的定义．平均数是所有数据的和除以数据的个数；一组数据中出现次数最多的数据叫做众数．也考查了条形统计图与用样本估计总体的思想．从条形图可以很容易看出数据的大小，从图形中获取正确信息是解题的关键．