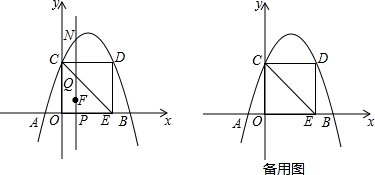题目内容
2.已知抛物线y=x2+bx-3与x轴交于A、B两点(A为左交点),与y轴的交于点C,tan∠BCO=$\frac{1}{3}$,(1)求抛物线的解析式.
(2)设点P是直线AC下方抛物线上的动点,设点P的横坐标为t,求以P、C、B为顶点的三角形的面积S与t的关系式.
(3)在第(2)问条件下,当S=3时,点M是直线PB上的动点,点N是直线BC上的动点,是否存在着使得以M、N、O、C为顶点的四边形为平行四边形?若存在请求出点M的坐标;若不存在,请说明理由.
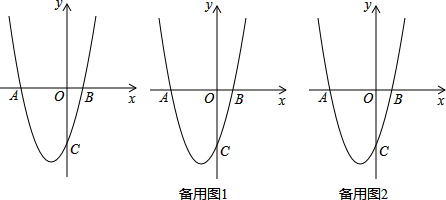
分析 (1)利用C(0,-3),tan∠BCO=$\frac{1}{3}$,可求出点B的坐标,代入y=x2+bx-3可求出b的值;
(2)作PH⊥OA,由S=S四边形APCB-S△APB=S△AHP+S梯形PHOC+S△BOC-S△APB可得到S与t的关系式;
(3)由S=3可求出t的值,得到点P的坐标,用待定系数法求出直线PB、BC的解析式,由点M是直线PB上的动点,点N是直线BC上的动点,使得以M、N、O、C为顶点的四边形为平行四边形,可知OM∥BC,求出PB和OM的交点即为所求.
解答 解:(1)∵y=x2+bx-3与y轴的交于点C,
∴C(0,-3),
∴OC=3,
∵tan∠BCO=$\frac{1}{3}$,
∴OB=1,
∴B(1,0)
代入y=x2+bx-3得,b=2,
∴y=x2+2x-3;
(2)如备用图1,作PH⊥OA,
∵y=x2+2x-3,
∴A(-3,0),P(t,t2+2t-3),
∴AH=t+3,OH=-t,AB=4,PH=-(t2+2t-3),
∵S=S四边形APCB-S△APB
=S△AHP+S梯形PHOC+S△BOC-S△APB
=$\frac{1}{2}$×AH×PH+$\frac{1}{2}$×OH×(PH+OC)+$\frac{1}{2}$×OB×OC-$\frac{1}{2}$×AB×PH
=$\frac{1}{2}$×(t+3)×[-(t2+2t-3)]+$\frac{1}{2}$×(-t)×[-(t2+2t-3)+3)+$\frac{1}{2}$×1×3-$\frac{1}{2}$×4×[-(t2+2t-3)]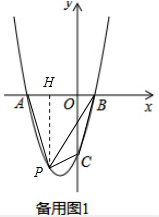
=$\frac{1}{2}$t2-$\frac{1}{2}$t;
(3)存在,如备用图2,过O作OM∥BC,交PB于点M,
当S=3时,3=$\frac{1}{2}$t2-$\frac{1}{2}$t,
解得:t=-2或t=3(舍去)
∴P(-2,-3)
设直线PB的解析式为yPB=kx+b,代入P、B两点坐标得,
$\left\{\begin{array}{l}{k+b=0}\\{-2k+b=-3}\end{array}\right.$
解得:k=1,b=-1,
∴yPB=x-1,
设直线CB的解析式为yBC=kx+b,代入C、B两点坐标得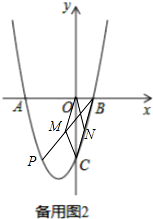
$\left\{\begin{array}{l}{k+b=0}\\{b=-3}\end{array}\right.$
解得:k=3,b=-3,
∴yBC=3x-3,
∵点M是直线PB上的动点,点N是直线BC上的动点,以M、N、O、C为顶点的四边形为平行四边形,
①OM∥BC时,
∴yOM=3x,
∵PB于OM交于点M,
∴x-1=3x
解得:x=-$\frac{1}{2}$,
∴y=-$\frac{3}{2}$,
∴M(-$\frac{1}{2}$,-$\frac{3}{2}$).
②NM∥OC时,此时有yN-yM=OC=3,
即(3x-3)-(x-1)=3,
解得x=$\frac{5}{2}$
故M($\frac{5}{2},\frac{3}{2}$).
综上,所求M点的坐标为(-$\frac{1}{2}$,-$\frac{3}{2}$)或($\frac{5}{2},\frac{3}{2}$).
点评 本题主要考查了待定系数法求二次函数和一次函数解析式、数形结合列函数表达式、以及平行四边形的判定,能够熟练的运用数形结合思想是解决问题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案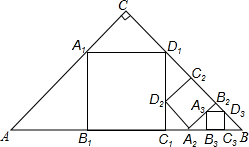 如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.
如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.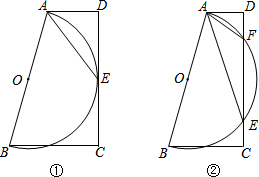 在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.
在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.