题目内容
7.在日常生活中取款,上网等都需要密码,有一种“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.若对于x4y+xy4因式分解的结果是xy(x+y)(x2-xy+y2),若xy与(x+y)构成的密码是127,则(x2-xy+y2)对应的数字是多少13.分析 因为第一位因式码xy和第二位因式码(x+y)构成的数是“127”,不可能出现xy=1,x+y=27,所以得出xy=12,x+y=7,由此整理代数式x2-xy+y2,整体代入求得答案即可.
解答 解:∵第一位因式码xy和第二位因式码(x+y)构成的数是“127”,
∴xy=12,x+y=7,
∴x2-xy+y2
=(x+y)2-3xy
=13.
故答案为:13.
点评 本题考查了因式分解的应用,理解题意,正确利用基本因式分解方法解决问题.

练习册系列答案
相关题目
15.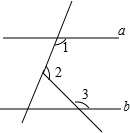 如图,a∥b,∠1=115°,∠2=95°,则∠3为( )
如图,a∥b,∠1=115°,∠2=95°,则∠3为( )
 如图,a∥b,∠1=115°,∠2=95°,则∠3为( )
如图,a∥b,∠1=115°,∠2=95°,则∠3为( )| A. | 120° | B. | 135° | C. | 150° | D. | 145° |
17.下列计算正确的是( )
| A. | $\sqrt{4}$$+\sqrt{(-2)^{2}}$=0 | B. | $\sqrt{\frac{3}{2}}$$-\sqrt{\frac{2}{3}}$=0 | C. | $\sqrt{6}$$÷\sqrt{3}$=2 | D. | $\sqrt{6}$×$\sqrt{\frac{3}{2}}$=3 |
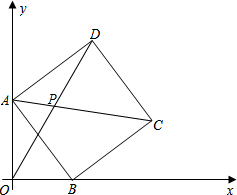 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,AC,OD交于点P,其中OA=4,OB=3.