题目内容
7．
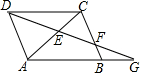已知：如图，?ABCD中，G是AB延长线上的一点，连接DG分别与AC、BC交于点E，F．（1）图中与△FBG相似的三角形为△DAG和△FCD；
（2）判断△AEG与△CED是否相似，并说明理由．
分析 （1）利用平行四边形的性质得BF∥AD，则可判断△FBG∽△DAG；利用平行四边形的性质得CD∥BG，则可判断△FBG∽△FCD；
（2）利用平行四边形的性质得CD∥AG，则可判断△AEG∽△CED．
解答 解：（1）因为BF∥AD，CD∥BG，所以△DAG和△FCD与△FBG相似．
故答案为△DAG和△FCD；
（2）△AEG∽△CED．理由如下：
∵四边形ABCD为平行四边形，
∴CD∥AB，即CD∥AG，
∴△AEG∽△CED．
点评 本题考查了相似三角形的判断：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似．
练习册系列答案
特高级教师点拨系列答案
相关题目
18．无论x为何值，下列各分式中总有意义的是（ ）
| A． | $\frac{1}{2x+1}$ | B． | $\frac{x}{2x+1}$ | C． | $\frac{3x+1}{{x}^{2}}$ | D． | $\frac{{x}^{2}}{2{x}^{2}+1}$ |
15．观察分析下列数据，寻找规律：$\sqrt{3}$，$\sqrt{6}$，3，$2\sqrt{3}$，$\sqrt{15}$，$3\sqrt{2}$，…那么第25个数据应是5$\sqrt{3}$．
19．若n满足（n-2015）2+（2016-n）2=1，则（n-2015）（2016-n）=（ ）
| A． | -1 | B． | 0 | C． | $\frac{1}{2}$ | D． | 1 |
17．
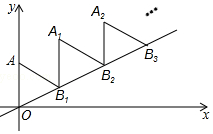如图，放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在Y轴上，点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上，则点A2016的坐标为（ ）
如图，放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在Y轴上，点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上，则点A2016的坐标为（ ）| A． | （2016$\sqrt{3}$，2018） | B． | （2016$\sqrt{3}$，2016） | C． | （2016，2016$\sqrt{3}$） | D． | （2016，2018$\sqrt{3}$） |