题目内容
17.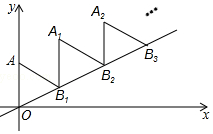 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在Y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2016的坐标为( )
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在Y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2016的坐标为( )| A. | (2016$\sqrt{3}$,2018) | B. | (2016$\sqrt{3}$,2016) | C. | (2016,2016$\sqrt{3}$) | D. | (2016,2018$\sqrt{3}$) |
分析 过B1作B1C⊥x轴,垂足为C,由条件可求得∠B1OC=30°,利用直角三角形的性质可求得B1C=1,OC=$\sqrt{3}$,可求得B1的坐标,同理可求得B2、B3的坐标,则可得出规律,可求得B2016的坐标.
解答 解: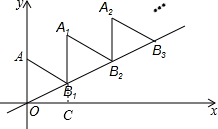 如图,过B1作B1C⊥x轴,垂足为C,
如图,过B1作B1C⊥x轴,垂足为C,
∵△OAB1是等边三角形,且边长为2,
∴∠AOB1=60°,OB1=2,
∴∠B1OC=30°,
在RtB1OC中,可得B1C=1,OC=$\sqrt{3}$,
∴B1的坐标为($\sqrt{3}$,1),
同理B2(2$\sqrt{3}$,2)、B3(3$\sqrt{3}$,3),
∴Bn的坐标为(n$\sqrt{3}$,n),
∴B2016的坐标为(2016$\sqrt{3}$,2016),
∴A2016的坐标为(2016$\sqrt{3}$,2018),
故选A.
点评 本题为规律型题目,利用等边三角形和直角三角形的性质求得B1的坐标,从而总结出点的坐标的规律是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
8.若(2a-1)2+2|b-3|=0,则ab=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | 6 |
5.下列运算正确的是( )
| A. | 3a+2a=6a | B. | a2+a3=a5 | C. | a6÷a2=a4 | D. | a2•a4=a8 |
12. 有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )
 有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )| A. | a+b>0 | B. | a-b=0 | C. | a+b<0 | D. | a-b>0 |
6.下列命题是假命题的是( )
| A. | 三角形的内心到三角形三条边的距离相等 | |
| B. | 三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等 | |
| C. | 对于实数a,b,若|a|≤|b|,则a≤b | |
| D. | 对于实数x,若$\sqrt{{x}^{2}}$=x,则x≥0 |
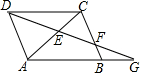 已知:如图,?ABCD中,G是AB延长线上的一点,连接DG分别与AC、BC交于点E,F.
已知:如图,?ABCD中,G是AB延长线上的一点,连接DG分别与AC、BC交于点E,F.