题目内容
2.在一个不透明的口袋中装有黑、白两种颜色的球,其中5个白球,若干个黑球,它们除颜色外完全相同,从中随机摸出一个球,记下颜色后放回,重复以上过程,经过多次实验发现摸到白球的频率稳定在0.2附近,据此估计袋中黑球的个数约为20个.分析 由摸到白球的频率稳定在0.2附近得出口袋中得到白色球的概率,进而求出黑球个数即可.
解答 解:设黑球个数为:x个,
∵摸到白色球的频率稳定在0.2左右,
∴口袋中得到白色球的概率为0.2,
∴$\frac{5}{5+x}$=0.2,
解得:x=20,
故黑球的个数为20个.
故答案为:20.
点评 此题主要考查了利用频率估计概率,根据大量反复试验下频率稳定值即概率得出是解题关键.

练习册系列答案
相关题目
12.在学习三角形时,李峰同学发现可以折叠出三角形的高,他在折叠其中一个三角形纸片时,只能折叠出一条高,这个纸片的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形或钝角三角形 |
13.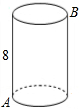 如图,一圆柱高8cm,底面圆的半径2cm,一只蚂蚁从点A爬到点B处吃食物(A、B恰为互相平行的直径的两个端点),要爬行的最短路程(π取3)是( )
如图,一圆柱高8cm,底面圆的半径2cm,一只蚂蚁从点A爬到点B处吃食物(A、B恰为互相平行的直径的两个端点),要爬行的最短路程(π取3)是( )
 如图,一圆柱高8cm,底面圆的半径2cm,一只蚂蚁从点A爬到点B处吃食物(A、B恰为互相平行的直径的两个端点),要爬行的最短路程(π取3)是( )
如图,一圆柱高8cm,底面圆的半径2cm,一只蚂蚁从点A爬到点B处吃食物(A、B恰为互相平行的直径的两个端点),要爬行的最短路程(π取3)是( )| A. | 20cm | B. | 10cm | C. | 14cm | D. | 无法确定 |
11.三角形中,到三个顶点距离相等的点是( )
| A. | 三边垂直平分线的交点 | B. | 三条中线的交点 | ||
| C. | 三条角平分线的交点 | D. | 三条高线的交点 |
12. 有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )
 有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的对应的位置如图所示,则下列结论正确的是( )| A. | a+b>0 | B. | a-b=0 | C. | a+b<0 | D. | a-b>0 |
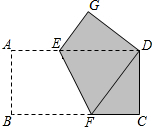 如图,矩形ABCD中,AB=2,AD=4,将矩形沿FE折叠,使点B与点D重合,点A的对应点是点G,则图中阴影部分的面积为$\frac{11}{2}$.
如图,矩形ABCD中,AB=2,AD=4,将矩形沿FE折叠,使点B与点D重合,点A的对应点是点G,则图中阴影部分的面积为$\frac{11}{2}$. 补全如图的数轴,并在数轴上标出绝对值大于1且小于4的所有负整数对应的点.
补全如图的数轴,并在数轴上标出绝对值大于1且小于4的所有负整数对应的点.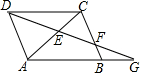 已知:如图,?ABCD中,G是AB延长线上的一点,连接DG分别与AC、BC交于点E,F.
已知:如图,?ABCD中,G是AB延长线上的一点,连接DG分别与AC、BC交于点E,F.