题目内容
方程2x+3y=10的正整数解是 .
考点:解二元一次方程
专题:
分析:当没有条件限制时,方程的解有无数个,所以方程2x+3y=10有无数个解,移项得x,根据题意可知0<y<
,且是整数.所以y=2,应的x=2.
| 10 |
| 3 |
解答:解:没有条件限制时,方程的解有无数个,
∴方程2x+3y=10,
移项得:x=
,
根据题意可知0<y<
,且是整数.
所以y=2,
对应的x=2,
故答案为:
.
∴方程2x+3y=10,
移项得:x=
| 10-3y |
| 2 |
根据题意可知0<y<
| 10 |
| 3 |
所以y=2,
对应的x=2,
故答案为:
|
点评:本题考查了二元一次方程的解的定义和求不定方程的整数解.当没有条件限制时,方程的解有无数个.求不定方程的整数解,先将方程做适当变形,确定其中一个未知数的取值范围,然后列举出适合条件的所有整数值,再求出另一个未知数的值.

练习册系列答案
相关题目
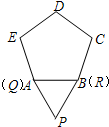 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )A、
| ||
B、
| ||
| C、8π | ||
| D、16π |
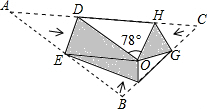 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )| A、78° | B、102° |
| C、120° | D、112° |
 如图,在⊙O中,
如图,在⊙O中, |
| AD |
 |
| BC |
| A、70° | B、35° |
| C、60° | D、30° |
若一组数据x1、x2、x3、x4、x5的平均数是a,则另一组数据x1、x2+1、x3+2、x4+3、x5+4的平均数是( )
| A、a | ||
| B、a+2 | ||
C、a+
| ||
| D、a+10 |
设A(-1,y1)、B(1,y2)、C(3,y3)是抛物线y=-
(x-
)2+k上的三个点,则y1、y2、y3的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y2<y3<y1 |
下列用等式的性质变形的方程,正确的是( )
A、
| ||||
B、
| ||||
| C、-2y=-5变成4y=10 | ||||
| D、3y-5=6变成3y=6-5 |
已知关于x的方程mx+2=2(m-x)的解满足2(x-
)-1=0,则m的值为( )
| 1 |
| 2 |
| A、-4 | B、-2 | C、2 | D、4 |