题目内容
若关于x的方程x2-2mx+5=0有实数根,则m的值可以是 .(任意给出一个符合条件的值即可)
考点:根的判别式
专题:开放型
分析:先根据关于x的方程x2-2mx+5=0有实数根得出△≥0,求出△的取值范围,找出符合条件的m的一个值即可.
解答:解:∵关于x的方程x2-2mx+5=0有实数根,
∴△≥0,即△=4m2-20≥0,解得m≥
或m≤-
,
∴m的值可以是3.
故答案为:3(答案不唯一).
∴△≥0,即△=4m2-20≥0,解得m≥
| 5 |
| 5 |
∴m的值可以是3.
故答案为:3(答案不唯一).
点评:本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△的关系是解答此题的关键.

练习册系列答案
相关题目
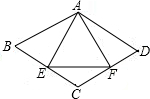 如图,在菱形ABCD内作一个等边△AEF,AE=AB.
如图,在菱形ABCD内作一个等边△AEF,AE=AB. 用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.
用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.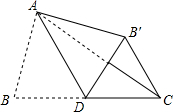 如图,在△ABC中,BC=5,AD为BC边上的中线,∠ADB=60°,将△ABD沿线段AD翻折,点B翻折到点B′的位置,连接CB′,则CB′的长为( )
如图,在△ABC中,BC=5,AD为BC边上的中线,∠ADB=60°,将△ABD沿线段AD翻折,点B翻折到点B′的位置,连接CB′,则CB′的长为( ) 如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.
如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置. 如图,直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的方程k1x+b=k2x+c的解x=
如图,直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的方程k1x+b=k2x+c的解x=