题目内容
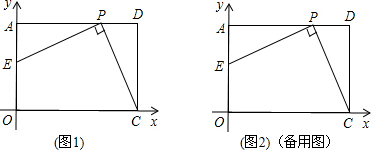
7.如图,在平面直角坐标系xOy中,点O为坐标原点,矩形AOCD的边OC、OA分别在x轴、y轴上,点D的坐标为(6,4),点P是线段AD边上的任意一点(不含端点A、D),连结PC,过点P作PE⊥PC交AO于E点.(1)当点P坐标为(4,4)时,求点E的坐标;
(2)当点P坐标为(5,4)时,在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)当点P在AD上运动时,对应的点E也随之在AO上运动,求OE的取值范围.
分析 (1)根据题意证明△APE≌△DCP即可;
(2)假设存在这样的点Q,根据△APE∽△DCP求出AE的长,再根据△QAE∽△CDQ列出比例式,求出AQ;
(3)设AP=x,AE=y,根据△APE∽△DCP,得到y与x的函数关系式,求出函数最大值得到答案.
解答 解:(1)∵∠EAD=∠EPC=∠PDC,
∴∠APE=∠DCP,
$\left\{\begin{array}{l}{∠APE=∠DCP}\\{AP=CD}\\{∠PAE=∠CDP}\end{array}\right.$,
∴△APE≌△DCP,
∴AE=PD=2,
∴点E(0,2);
(2)存在这样的点Q,
假设存在这样的点Q,
∵∠EAP=∠EPC=∠PDC,
∴△APE∽△DCP,
∴$\frac{AP}{DC}$=$\frac{AE}{DP}$,
∵AP=5,CD=4,DP=1,
∴AE=$\frac{5}{4}$,
∵∠EAQ=∠EQC=∠QDC,
∴△QAE∽△CDQ,
∴$\frac{AQ}{CD}$=$\frac{AE}{DQ}$,
设AQ=x,$\frac{x}{4}$=$\frac{\frac{4}{5}}{6-x}$,
解得x=1或x=5,当x=5时点Q与点P重合,故舍去,
所以存在这样的点Q,其坐标为(1,4);
(3)设AP=x,AE=y,
∵△APE∽△DCP,
∴$\frac{AP}{DC}$=$\frac{AE}{DP}$,
∴$\frac{x}{4}$=$\frac{y}{6-x}$,
∴$y=-\frac{1}{4}{x^2}+\frac{3}{2}x$,
当x=3时(在0<x<6范围内),y最大值=$\frac{9}{4}$,
又∵E在AB上运动,且AO=4,
∴OE的最小值为4-$\frac{9}{4}$=$\frac{7}{4}$,
∴OE的取值范围是$\frac{7}{4}$≤BE<4.
点评 本题考查的是矩形的性质和相似三角形的判定和性质,掌握性质并灵活运用性质进行解答是解题的关键,注意二次函数最值的确定方法.

 备战中考寒假系列答案
备战中考寒假系列答案 如图,AB∥CD,∠BED=70°,BC平分∠ABE,则∠C的度数为( )
如图,AB∥CD,∠BED=70°,BC平分∠ABE,则∠C的度数为( )| A. | 105° | B. | 70° | C. | 35° | D. | 17.5° |
| A. | $\left\{\begin{array}{l}x=6\\ y=10\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=6\\ y=-10\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=-6\\ y=10\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-6\\ y=-10\end{array}\right.$ |
 如图,一艘轮船位于灯塔P的北偏东45°方向,距灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东35°方向上的B处.这时,轮船所在的B处距离灯塔P有多远?(精确到0.1海里)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
如图,一艘轮船位于灯塔P的北偏东45°方向,距灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东35°方向上的B处.这时,轮船所在的B处距离灯塔P有多远?(精确到0.1海里)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)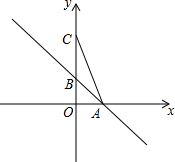 如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B.点C在y轴的正半轴上,且sin∠ACB=$\frac{\sqrt{10}}{10}$
如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B.点C在y轴的正半轴上,且sin∠ACB=$\frac{\sqrt{10}}{10}$  如图,射线AB,CD分别与直线l相交于点G、H,若∠1=∠2,∠C=65°,则∠A的度数是115°.
如图,射线AB,CD分别与直线l相交于点G、H,若∠1=∠2,∠C=65°,则∠A的度数是115°. 如图,过反比例函数y=$\frac{k}{x}$图象上三点A、B、C分别作直角三角形和矩形,图中S1+S2=5,则S3=5.
如图,过反比例函数y=$\frac{k}{x}$图象上三点A、B、C分别作直角三角形和矩形,图中S1+S2=5,则S3=5.