题目内容
18．
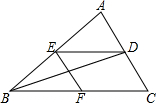如图：△ABC中，BD平分∠ABC，DE∥BC，∠EFB=∠C，判断BE与FC的数量关系，并说明理由．
分析 先证明四边形CDEF是平行四边形，得出DE=CF，再由平行线的性质和角平分线得出∠EDB=∠EBD，证出BE=DE，即可得出结论．
解答 解：BE=FC；理由如下：
∵∠EFB=∠C，
∴CD∥EF，
∵DE∥BC，
∴四边形CDEF是平行四边形，∠EDB=∠CBD，
∵∴DE=CF，
∵BD平分∠ABC，
∴∠CBD=∠EBD，
∴∠EDB=∠EBD，
∴BE=DE，
∴BE=CF．
点评 本题考查了平行四边形的判定与性质、等腰三角形的判定；熟练掌握平行四边形的判定与性质，并能进行推理论证是解决问题的关键．
练习册系列答案
寒假学与练系列答案
相关题目
8．无论x取什么数时，总有意义的分式是（ ）
| A． | $\frac{2x}{{{x^2}+0.2}}$ | B． | $\frac{x}{2x+1}$ | C． | $\frac{3x}{{{x^3}+1}}$ | D． | $\frac{x-5}{x^2}$ |
如图，已知线段a和线段b，根据要求作图．