题目内容
7.解下列方程①2(x-1)2=$\sqrt{64}$
②-27(x-1)3=-64
③4x2=$\frac{49}{25}$.
分析 ①根据平方根的定义,即可解答;
②根据立方根的定义,即可解答;
③根据平方根的定义,即可解答.
解答 解:①2(x-1)2=$\sqrt{64}$
2(x-1)2=8
(x-1)2=4
x-1=±2
x=3或x=-1.
②-27(x-1)3=-64
$(x-1)^{3}=\frac{64}{27}$
x-1=$\frac{4}{3}$
x=$\frac{5}{3}$
③4x2=$\frac{49}{25}$
2x=$±\frac{7}{5}$
x=$±\frac{7}{10}$.
点评 本题考查了平方根、立方根,解决本题的关键是熟记平方根、立方根.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
15.下列说法正确的是( )
| A. | $\frac{8}{27}$的立方根是±$\frac{2}{3}$ | B. | -125没有立方根 | ||
| C. | -1的平方的立方根是1 | D. | $\root{3}{9}$=3 |
12.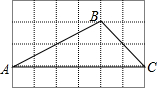 如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
 如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{1}{3}$ |
19.已知反比例函数y=$\frac{k}{x}$的图象位于第一、第三象限,则k的取值范围是( )
| A. | k≥0 | B. | k>0 | C. | k≤0 | D. | k<0 |
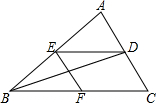 如图:△ABC中,BD平分∠ABC,DE∥BC,∠EFB=∠C,判断BE与FC的数量关系,并说明理由.
如图:△ABC中,BD平分∠ABC,DE∥BC,∠EFB=∠C,判断BE与FC的数量关系,并说明理由. 如图,直线y=kx(k>0)与双曲线y=$\frac{1}{x}$交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=$\frac{1}{2}$.其中正确结论是①②③(填序号)
如图,直线y=kx(k>0)与双曲线y=$\frac{1}{x}$交于A、B两点,BC⊥x轴于C,连接AC交y轴于D,下列结论:①A、B关于原点对称;②△ABC的面积为定值;③D是AC的中点;④S△AOD=$\frac{1}{2}$.其中正确结论是①②③(填序号)