题目内容
9. 如图,在?ABCD中,已知AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,求OB的长.
如图,在?ABCD中,已知AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,求OB的长.
分析 由AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,直接利用勾股定理求解即可求得AC的长,然后由平行四边形的性质,求得OA的长,再利用勾股定理,求得OB的长.
解答 解:∵AB=$\sqrt{3}$,BC=$\sqrt{7}$,∠BAC=90°,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=2,
∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC=1,
∴OB=$\sqrt{A{B}^{2}+O{A}^{2}}$=2.
点评 此题考查了平行四边形的性质以及勾股定理.注意掌握平行四边形的对角线互相平分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 现有一块长7.5cm,宽5cm的木板,能否在这块木板上截出两个面积分别为8cm2和18cm2的正方形木板?请通过计算说明.
现有一块长7.5cm,宽5cm的木板,能否在这块木板上截出两个面积分别为8cm2和18cm2的正方形木板?请通过计算说明.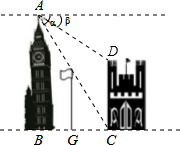 如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.