题目内容
3.已知一次函数y=kx+b的图象经过点A(5,3)和B(-3,-1).(1)求k与b的值.
(2)将此函数的图象沿x轴方向平移多少个单位,才能使它经过坐标原点.
分析 (1)将点A(5,3)和B(-3,-1)分别代入一次函数解析式y=kx+b,列出关于k、b的方程组,通过解方程组即可求得该函数的解析式;
(2)先根据平移时k的值不变,只有b发生变化,可知将y=$\frac{1}{2}$x+$\frac{1}{2}$平移后的解析式y=$\frac{1}{2}$x的图象经过坐标原点,又y=$\frac{1}{2}$x+$\frac{1}{2}$=$\frac{1}{2}$(x+1),根据左加右减的平移法则即可求解.
解答 解:(1)根据题意,得
$\left\{\begin{array}{l}{5k+b=3}\\{-3k+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$,
则一次函数的解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$;
(2)∵平移时k的值不变,只有b发生变化,
∴y=$\frac{1}{2}$x的图象经过坐标原点,
∵y=$\frac{1}{2}$x+$\frac{1}{2}$=$\frac{1}{2}$(x+1),
∴将一次函数y=$\frac{1}{2}$x+$\frac{1}{2}$的图象向右平移1个单位后的解析式为:y=$\frac{1}{2}$(x+1-1),即y=$\frac{1}{2}$x.
故将此函数的图象沿x轴方向向右平移1个单位,能使它经过坐标原点.
点评 本题考查了待定系数法求一次函数的解析式、一次函数图象与几何变换.解题的关键是待定系数法求函数解析式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目


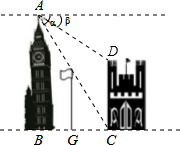 如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.