题目内容
1.阅读下面的材料,并解答后面的问题:$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}$-$\sqrt{3}$
(1)观察上面的等式,请直接写出$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数)的结果$\sqrt{n+1}$-$\sqrt{n}$;
(2)计算($\sqrt{n+1}+\sqrt{n}$)($\sqrt{n+1}-\sqrt{n}$)=1;
(3)请利用上面的规律及解法计算:($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2016}}$)($\sqrt{2017}+1$).
分析 (1)利用分母有理化的方法解答;
(2)根据平方差公式计算即可;
(3)利用阅读材料的结论和二次根式的加减混合运算法则计算.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$,
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)($\sqrt{n+1}+\sqrt{n}$)($\sqrt{n+1}-\sqrt{n}$)=($\sqrt{n+1}$)2-($\sqrt{n}$)2=1,
故答案为:1;
(3)($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2016}}$)($\sqrt{2017}+1$)
=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2017}$-$\sqrt{2016}$)($\sqrt{2017}+1$)
=($\sqrt{2017}$-1)($\sqrt{2017}$+1)
=2017-1
=2016.
点评 本题考查的是分母有理化的应用,掌握平方差公式、二次根式的性质是解题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
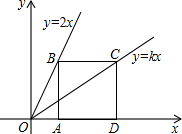 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.
如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm. 如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.
如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$. 如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α.
如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α. 将长为20cm,宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为y=17x+3.
将长为20cm,宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为y=17x+3.