题目内容
解方程:
+
=
+
.
| x-4 |
| x-5 |
| x-8 |
| x-9 |
| x-7 |
| x-8 |
| x-5 |
| x-6 |
考点:解分式方程
专题:计算题
分析:分式方程变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:方程变形得:
+
=
+
,即
+
=
+
,
整理得:
=
,即
=
,
当2x-14=0,即x=7时,方程成立;
当2x-14≠0,即x≠7时,方程无解,
经检验x=7是分式方程的解.
| x-5+1 |
| x-5 |
| x-9+1 |
| x-9 |
| x-8+1 |
| x-8 |
| x-6+1 |
| x-6 |
| 1 |
| x-5 |
| 1 |
| x-9 |
| 1 |
| x-8 |
| 1 |
| x-6 |
整理得:
| x-9+x-5 |
| x2-14x+45 |
| x-6+x-8 |
| x2-14x+48 |
| 2x-14 |
| x2-14x+45 |
| 2x-14 |
| x2-14x+48 |
当2x-14=0,即x=7时,方程成立;
当2x-14≠0,即x≠7时,方程无解,
经检验x=7是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
下列各计算题中,结果是零的是( )
| A、(+3)-|-3| | ||||
| B、|+3|+|-3| | ||||
| C、-3[-(-3)] | ||||
D、
|
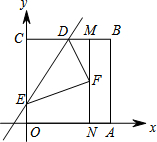 如图,四边形OABC是一张边长为4的正方形纸片,将其放在平面直角坐标系中,使得点O与坐标原点重合,点A、C分别在x轴、y轴的正半轴上,D为BC中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与BD交于点M.现将纸片沿过D点的直线折叠,使顶点C落在线段MN上的点F处,折痕与y轴的交点记为E.
如图,四边形OABC是一张边长为4的正方形纸片,将其放在平面直角坐标系中,使得点O与坐标原点重合,点A、C分别在x轴、y轴的正半轴上,D为BC中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与BD交于点M.现将纸片沿过D点的直线折叠,使顶点C落在线段MN上的点F处,折痕与y轴的交点记为E.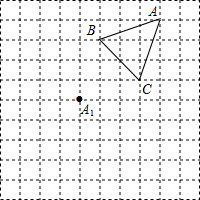 在正方形网格中,每个小正方形的边长均为1个单位长度.△ABC三个顶点的位置如图所示,将点A平移到A1,点B平移到B1,点C平移到C1.
在正方形网格中,每个小正方形的边长均为1个单位长度.△ABC三个顶点的位置如图所示,将点A平移到A1,点B平移到B1,点C平移到C1. 已知:如图,在?ABCD中,点E,F分别在AB和CD,BE=DF.求证:四边形DEBF是平行四边形.
已知:如图,在?ABCD中,点E,F分别在AB和CD,BE=DF.求证:四边形DEBF是平行四边形.