题目内容
解方程:
(1)(x+4)2=5(x+4);
(2)(x+1)2=4x.
(1)(x+4)2=5(x+4);
(2)(x+1)2=4x.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)首先移项,利用提取公因式法分解因式进而解方程得出即可;
(2)首先去括号进而合并同类项,再利用公式法解方程得出即可.
(2)首先去括号进而合并同类项,再利用公式法解方程得出即可.
解答:解:(1)(x+4)2=5(x+4)
(x+4)2-5(x+4)=0
则(x+4)[(x+4)-5]=0
故x+4=0或x-1=0,
解得:x1=-4,x2=1;
(2)(x+1)2=4x
整理得出:x2-2x+1-4x=0,
则x2-6x+1=0,
∵b2-4ac=36-4=32>0,
∴x=
,
解得;x1=3+2
,x2=3-2
.
(x+4)2-5(x+4)=0
则(x+4)[(x+4)-5]=0
故x+4=0或x-1=0,
解得:x1=-4,x2=1;
(2)(x+1)2=4x
整理得出:x2-2x+1-4x=0,
则x2-6x+1=0,
∵b2-4ac=36-4=32>0,
∴x=
6±4
| ||
| 2 |
解得;x1=3+2
| 2 |
| 2 |
点评:此题主要考查了因式分解法和公式法解一元二次方程,熟练记忆公式法解方程是解题关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
下列说法正确的是( )
| A、一个数不是正数就是负数 |
| B、一个数的绝对值一定是正数 |
| C、在有理数中,没有最大的数 |
| D、不存在相反数等于本身的数 |
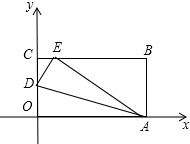 如图,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.
如图,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.