题目内容
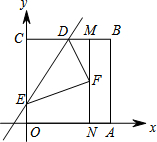 如图,四边形OABC是一张边长为4的正方形纸片,将其放在平面直角坐标系中,使得点O与坐标原点重合,点A、C分别在x轴、y轴的正半轴上,D为BC中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与BD交于点M.现将纸片沿过D点的直线折叠,使顶点C落在线段MN上的点F处,折痕与y轴的交点记为E.
如图,四边形OABC是一张边长为4的正方形纸片,将其放在平面直角坐标系中,使得点O与坐标原点重合,点A、C分别在x轴、y轴的正半轴上,D为BC中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与BD交于点M.现将纸片沿过D点的直线折叠,使顶点C落在线段MN上的点F处,折痕与y轴的交点记为E.(1)求点F的坐标和∠FDM的大小;
(2)求直线DE的解析式;
(3)点P在直线DE上,且△PEF为等腰三角形,请直接写出点P的坐标.
考点:一次函数综合题
专题:
分析:(1)根据勾股定理求得MF的长,即可求得F的坐标,解直角三角形DMF,根据sin∠FDM=
=
,即可求得∠FDM的大小;
(2)解直角三角形CDE,求得CE的长,即可求得E的坐标,应用待定系数法即可求得直线DE的解析式;
(3)分三种情况讨论求得.
| DM |
| DF |
| ||
| 2 |
(2)解直角三角形CDE,求得CE的长,即可求得E的坐标,应用待定系数法即可求得直线DE的解析式;
(3)分三种情况讨论求得.
解答:解:(1)∵D为BC中点,
∴CD=2,
∴D(2,4),DM=1,
在RT△DMF中,DM=1,DF=CD=2,
∴MF=
=
,
∴FN=4-
,
∴F(3,4-
),
∵sin∠FDM=
=
,
∴∠FDM=60°.
(2)∵∠FDM=60°,
∴∠CDE=60°,
∴tan∠CDE=tan60°=
,
∴CE=
×2=2
,
∴OE=4-2
,
∴E(0,4-2
),
设直线DE的解析式为:y=kx+b,
∴
,
解得:
.
∴直线DE的解析式为:y=
x+4-2
;
(3)∵E(0,4-2
),F(3,4-
),
∴EF=
=2
,
设P(m,
m+4-2
),
当PE=EF时,则PE2=m2+(
m+4-2
-4+2
)2=4m2,
∵4m2=(2
)2,
解得:m=
,或m=-
,
当PE=PF时,∵PE2=4m2,PF2=(m-3)2+(
m+4-2
-4+
)2=4m2-12m+12,
∴4m2-12m+12=4m2,解得:m=1,
当PF=EF时,则4m2-12m+12=(2
)2,
解得:m=3,或m=0(舍去),
所以P的坐标为(
,7-2
)或(-
,1-2
)或(1,4-
)或(3,4+
).
∴CD=2,
∴D(2,4),DM=1,
在RT△DMF中,DM=1,DF=CD=2,
∴MF=
| DF2-DM2 |
| 3 |
∴FN=4-
| 3 |
∴F(3,4-
| 3 |
∵sin∠FDM=
| DM |
| DF |
| ||
| 2 |
∴∠FDM=60°.
(2)∵∠FDM=60°,
∴∠CDE=60°,
∴tan∠CDE=tan60°=
| CE |
| CD |
∴CE=
| 3 |
| 3 |
∴OE=4-2
| 3 |
∴E(0,4-2
| 3 |
设直线DE的解析式为:y=kx+b,
∴
|
解得:
|
∴直线DE的解析式为:y=
| 3 |
| 3 |
(3)∵E(0,4-2
| 3 |
| 3 |
∴EF=
32+(4-
|
| 3 |
设P(m,
| 3 |
| 3 |
当PE=EF时,则PE2=m2+(
| 3 |
| 3 |
| 3 |
∵4m2=(2
| 3 |
解得:m=
| 3 |
| 3 |
当PE=PF时,∵PE2=4m2,PF2=(m-3)2+(
| 3 |
| 3 |
| 3 |
∴4m2-12m+12=4m2,解得:m=1,
当PF=EF时,则4m2-12m+12=(2
| 3 |
解得:m=3,或m=0(舍去),
所以P的坐标为(
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了直线的交点坐标的求法,待定系数法求解析式,应用直角三角函数解直角三角形,勾股定理的应用,等腰三角形的性质等,(3)分三种情况讨论是本题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
下列说法正确的是( )
| A、有理数可以用有限小数或无限循环小数表示 |
| B、无限小数就是无理数 |
| C、不循环小数是无理数 |
| D、0既不是有理数,也不是无理数 |
有下列说法:
①不存在最大的无理数,也不存在最小的无理数;
②无限小数都是无理数;
③无理数都是无限小数;
④带根号的数都是无理数;
⑤两个无理数的和还是无理数;
⑥有绝对值最小的数;
⑦比负数大的是正数.
其中,错误的有( )
①不存在最大的无理数,也不存在最小的无理数;
②无限小数都是无理数;
③无理数都是无限小数;
④带根号的数都是无理数;
⑤两个无理数的和还是无理数;
⑥有绝对值最小的数;
⑦比负数大的是正数.
其中,错误的有( )
| A、3个 | B、4个 | C、5个 | D、6个 |