题目内容
13. 如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.
如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.(1)求证:AB∥CD.
(2)小明在完成(1)的证明后继续进行了探索,过点G作MN∥EF,分别交AB、CD于点M、N,过点H作PQ∥EF,分别交AB、CD于点P、Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形.请补全他的证明思路.
小明的证明思路:
由AB∥CD,MN∥EF,PQ∥EF易证,四边形MNQP是平行四边形.要证?MNQP是菱形,只要证MN=NQ.由已知条件FG平分∠CFE,MN∥EF,可得GN=FN,故只要证GM=FQ,即证△MGE≌△QFH,由于易证GE=FH,∠GME=∠FQH,故要证△MGE≌△QFH,只要证∠MGE=∠QFH,由∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证.
(3)请你再写出一条菱形的判定定理.
分析 (1)根据矩形的性质得到∠EGF=90°,根据角平分线的定义即可得到结论;
(2)利用菱形的判定方法首先得出要证?MNQP是菱形,只要证MN=NQ,再证∠MGE=∠QFH得出即可;
(3)写出写出一条菱形的判定定理即可.
解答 (1)证明:∵四边形EGFH为矩形,
∴∠EGF=90°,
∴∠GEF+∠GFE=90°,
∵GE,GF分别是∠AEF,∠NFE的平分线,
∴∠AEF+∠NFE=180°,
∴AB∥CD;
(2)解:由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,
要证?MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,
故只要证GM=FQ,即证△MGE≌△QFH,易证 GE=FH、∠GME=∠FQH,
故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证;
故答案为:FG平分∠CFE,GE=FH、∠GME=∠FQH,∠GEF=∠EFH;
(3)有一组邻边相等的平行四边形是菱形.
点评 此题主要考查了矩形的判定以及菱形的判定和角平分线的性质,根据题意得出证明菱形的方法是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
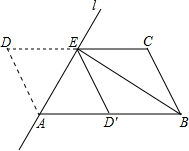 如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )
如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )