题目内容
8.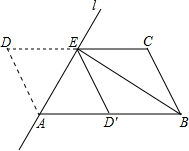 如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )
如图,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用平行线的性质以及角平分线的性质得出∠EAB+∠EBA=90°,再结合勾股定理得出答案.
解答 解:∵BE平分∠ABC,
∴∠CBE=∠EBA,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2,
∴AE=$\sqrt{{5}^{2}-{4}^{2}}$=3.
故选:B.
点评 此题主要考查了平行四边形的判定与性质以及勾股定理等知识,得出∠AEB=90°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列运算正确的是( )
| A. | x3+x2=x5 | B. | x3-x3=x0 | C. | x3÷x2=x | D. | (x3)2=x5 |
16.在下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.已知命题:“三角形外心一定不在三角形内部”,下列选项中,可以作为该命题是假命题的反例是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
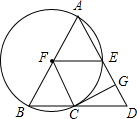 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G. 如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.
如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.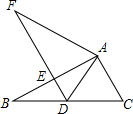 如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )
如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )