题目内容

18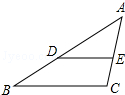．如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，AD=4，BD=2，求$\frac{DE}{BC}$的值．

分析 由平行判定△ADE∽△ABC，得出$\frac{AD}{AB}$=$\frac{DE}{BC}$，进一步求得答案即可．

解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，
∵AD=4，DB=2，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{4}{4+2}$=$\frac{2}{3}$，
∴$\frac{DE}{BC}$的值为$\frac{2}{3}$．

点评 此题考查相似三角形的判定与性质，掌握三角形的判定方法是解决问题的关键．

练习册系列答案
相关题目
8．在平面直角坐标系中，等腰三角形ABC的顶点A的坐标为（3，3）
（1）若底边BC在x轴上，
①点B的坐标为（-1，0），则满足条件的C点的坐标为（7，0）；
②设点B、点C的坐标分别为（m，0）、（n，0），则m、n应满足的条件为m+n=6；
（2）若底边BC的两端分别在x轴，y轴上，
①点B的坐标为（-1，0），则满足条件的C点的坐标为（0，-1），（0，7）；
②设点B、点C的坐标分别为（m，0）、（0，n），则m、n应满足怎样的条件？请说明理由．
9．把下列多项式分解因式
（1）x3-9x
（2）4a3-12a2+9a
（3）6x（a-b）+4y（b-a）                       
（4）9（a+b）2-25（a-b）2．
6．等腰三角形的腰长为10，底长为12，则其腰上的高为（　　）
A．13B．8C．9.6D．64
13．解方程组：$\left\{\begin{array}{l}{{x}^{2}+9{y}^{2}=4}\\{\sqrt{3}x+3y=2}\end{array}\right.$．
3．已知|a+2b-1|+（b+1）2=0，求代数式（$\frac{1}{a}$+$\frac{1}{b}$）-1+$\frac{（a+b）^{-2}}{{a}^{-2}-{b}^{-2}}$÷$\frac{（3a-1）^{-1}}{（-a）^{-2}{b}^{-1}}$的值．
10．如图，在直角坐标系中，直线AB与直线y=x相交于点A（3，a），与x轴的交点为B（9，0）．
（1）求a的值，以及直线AB的解析式；
（2）若有一动点M从原点出发，沿x轴正半轴向点B运动，过M作直线l⊥x轴，直线l与△OAB的另一边交点记为N，点O关于直线l作轴对称变换，对称点为Q，
①当MN=2时，求点Q的坐标；
②连结AQ，若△QAB为直角三角形，则此时的MN的长为1.5或$\frac{3}{4}$（直接写出答案）．
7．如果欲求1+3+32+33+…+320的值，可令S=1+3+32+33+…+320①
将①式两边同乘3，得3S=3+32+33+34+…+321②
由②式减去①式，得S=$\frac{{3}^{21}-1}{2}$．
8．已知二次函数y=-x2-14x+15，若自变量x分别取x1，x2，x3，且0＜x1＜x2＜x3，则对应的函数值y1，y2，y3的大小关系是y1＞y2＞y3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网