题目内容
3.已知|a+2b-1|+(b+1)2=0,求代数式($\frac{1}{a}$+$\frac{1}{b}$)-1+$\frac{(a+b)^{-2}}{{a}^{-2}-{b}^{-2}}$÷$\frac{(3a-1)^{-1}}{(-a)^{-2}{b}^{-1}}$的值.分析 根据非负数的性质求出a、b的值,代入代数式计算即可.
解答 解:∵|a+2b-1|+(b+1)2=0,
∴a+2b-1=0,b+1=0,
解得a=3,b=-1,
原式=$\frac{ab}{a+b}$+$\frac{1}{(a+b)^{2}}$•$\frac{{a}^{2}{b}^{2}}{(b+a)(b-a)}$•$\frac{3a-1}{{a}^{2}b}$=-$\frac{3}{2}$+$\frac{1}{4}$×$\frac{9}{8}$×$\frac{10}{9}$=-$\frac{19}{16}$.
点评 本题考查的是非负数的性质和代数式的化简求值,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
11.如果关于x的一元二次方程x2-4x+k=0有两个相等的实数根,那么k的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
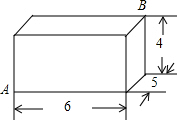 如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为$\sqrt{117}$cm.
如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为$\sqrt{117}$cm.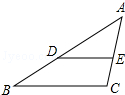 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=4,BD=2,求$\frac{DE}{BC}$的值.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=4,BD=2,求$\frac{DE}{BC}$的值.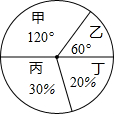 红星中学对今年中考数学成绩进行调研,将其成绩分成三类,其中甲类250人,请你画出条形统计图.
红星中学对今年中考数学成绩进行调研,将其成绩分成三类,其中甲类250人,请你画出条形统计图.