题目内容
6.等腰三角形的腰长为10,底长为12,则其腰上的高为( )| A. | 13 | B. | 8 | C. | 9.6 | D. | 64 |
分析 作AD⊥BC于D,由等腰三角形的三线合一性质得出BD=CD=$\frac{1}{2}$BC=6,∠ADB=90°,由勾股定理求出AD,由三角形面积的计算方法,求出BE的长即可.
解答 解:如图所示: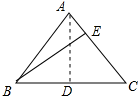
BE是等腰三角形的腰AC上的高,作AD⊥BC于D;
∵AB=AC,
∴BD=CD=$\frac{1}{2}$BC=6,∠ADB=90°,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴△ABC的面积=$\frac{1}{2}$×AC×BE=$\frac{1}{2}$×BC×AD,
∴AC×BE=BC×AD,
即10×BE=12×8,
解得:BE=9.6.
故选C.
点评 本题考查了等腰三角形的性质、勾股定理、三角形面积的计算方法;熟练掌握等腰三角形的性质,运用勾股定理和三角形的面积的计算方法是解决问题的关键.

练习册系列答案
相关题目
11.如果关于x的一元二次方程x2-4x+k=0有两个相等的实数根,那么k的值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
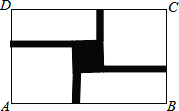 如图,某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的$\frac{1}{4}$,若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$,求道路的宽.
如图,某旅游景点要在长、宽分别为40m、24m的矩形水池的正中央建立一个与矩形的各边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的$\frac{1}{4}$,若道路与观赏亭的面积之和是矩形水池面积的$\frac{1}{6}$,求道路的宽.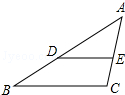 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=4,BD=2,求$\frac{DE}{BC}$的值.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=4,BD=2,求$\frac{DE}{BC}$的值.