题目内容
9.把下列多项式分解因式(1)x3-9x
(2)4a3-12a2+9a
(3)6x(a-b)+4y(b-a)
(4)9(a+b)2-25(a-b)2.
分析 (1)原式提取x,再利用平方差公式分解即可;
(2)原式提取a,再利用完全平方公式分解即可;
(3)原式变形后,提取公因式即可得到结果;
(4)原式平方差公式分解即可.
解答 解:(1)原式=x(x2-9)=x(x+3)(x-3);
(2)原式=a(4a2-12a+9)=a(2a-3)2;
(3)原式=6x(a-b)-4y(a-b)=2(a-b)(3x-2y);
(4)原式=[3(a+b)+5(a-b)][3(a+b)-5(a-b)]=4(4a-b)(-a+4b).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握运算法则是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
19. 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
4.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
由表可知当x>2时,y随x的增大而增大;当y<5时,x的取值范围是0<x<4.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
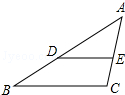 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=4,BD=2,求$\frac{DE}{BC}$的值.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=4,BD=2,求$\frac{DE}{BC}$的值.