题目内容
16.已知实数a,b满足$\sqrt{(a-1)^{2}}$+$\sqrt{(a-6)^{2}}$=10-|b-3|-|b-2|,则a2+b2的最大值为( )| A. | 50 | B. | 45 | C. | 40 | D. | 0 |
分析 化简二次根式,由$\sqrt{(a-1)^{2}}$+$\sqrt{(a-6)^{2}}$=10-|b-3|-|b-2|得到|a-1|+|a-6|+|b-3|+|b-2|=10,根据|a-1|+|a-6|≥5,|b+3|+|b-2|≥5,确定a、b的取值范围,计算出a2+b2的值.
解答 解:由$\sqrt{(a-1)^{2}}$+$\sqrt{(a-6)^{2}}$=10-|b-3|-|b-2|,
得|a-1|+|a-6|+|b-3|+|b-2|=10,
又∵|a-1|+|a-6|≥5,|b+3|+|b-2|≥5,
∵|a-1|+|a-6|=5,|b+3|+|b-2|=5,
则1≤a≤6,-3≤b≤2
∴a2+b2=62+32=45
故选B.
点评 本题考查了二次根式的化简、绝对值的化简,解决本题的关键是由|a-1|+|a-6|≥5,|b+3|+|b-2|≥5,确定a、b的取值范围.

练习册系列答案
相关题目
6.已知a、b是两个自然数,若a+b=10,则a×b的最大值为( )
| A. | 20 | B. | 21 | C. | 24 | D. | 25 |
11.如图,下面表格给出的是国外四个城市与北京的时差(带“+”表示同一时刻比北京时间早的时数),如果现在悉尼时间是下午6时,则伦敦时间是上午8点.
| 城市 | 纽约 | 悉尼 | 伦敦 | 罗马 |
| 时差/h | -13 | +2 | -8 | -7 |
1.对于正比例函数y=kx(k≠0),当自变量x的值减小2时,函数y的值减小-6,则k的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
 在一次运输任务中,一辆汽车将一批货物从深圳运往广州,到达广州卸货后返回,设汽车从深圳出发x(h)时,汽车与深圳的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
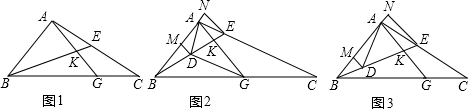
在一次运输任务中,一辆汽车将一批货物从深圳运往广州,到达广州卸货后返回,设汽车从深圳出发x(h)时,汽车与深圳的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题: 如图,已知∠1+∠2=180°,则图中与∠1相等的角共有3个.
如图,已知∠1+∠2=180°,则图中与∠1相等的角共有3个.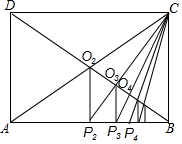 在美国的一堂数学课上,老师给同学们布置了一道“任意等分一条线段”的题.其中有一个学生用了一种与众不同的方法.他在纸上做出了如图所示的一个图形,他以老师给的已知线段AB为一条边作矩形ABCD,设AC、BD交于点O2,作O2P2⊥AB,则垂足P2就是AB的二等分点:连接CP2交BD于点O3,作O3P3⊥AB,则垂足P3就是AB的三等分点;再依次做下去,就得到AB的四等分点,…n等分点.你能用所学过的知识解释其中的缘由吗?
在美国的一堂数学课上,老师给同学们布置了一道“任意等分一条线段”的题.其中有一个学生用了一种与众不同的方法.他在纸上做出了如图所示的一个图形,他以老师给的已知线段AB为一条边作矩形ABCD,设AC、BD交于点O2,作O2P2⊥AB,则垂足P2就是AB的二等分点:连接CP2交BD于点O3,作O3P3⊥AB,则垂足P3就是AB的三等分点;再依次做下去,就得到AB的四等分点,…n等分点.你能用所学过的知识解释其中的缘由吗?