题目内容
20.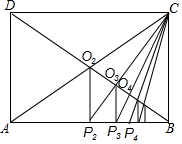 在美国的一堂数学课上,老师给同学们布置了一道“任意等分一条线段”的题.其中有一个学生用了一种与众不同的方法.他在纸上做出了如图所示的一个图形,他以老师给的已知线段AB为一条边作矩形ABCD,设AC、BD交于点O2,作O2P2⊥AB,则垂足P2就是AB的二等分点:连接CP2交BD于点O3,作O3P3⊥AB,则垂足P3就是AB的三等分点;再依次做下去,就得到AB的四等分点,…n等分点.你能用所学过的知识解释其中的缘由吗?
在美国的一堂数学课上,老师给同学们布置了一道“任意等分一条线段”的题.其中有一个学生用了一种与众不同的方法.他在纸上做出了如图所示的一个图形,他以老师给的已知线段AB为一条边作矩形ABCD,设AC、BD交于点O2,作O2P2⊥AB,则垂足P2就是AB的二等分点:连接CP2交BD于点O3,作O3P3⊥AB,则垂足P3就是AB的三等分点;再依次做下去,就得到AB的四等分点,…n等分点.你能用所学过的知识解释其中的缘由吗?
分析 根据四边形ABCD是矩形,得到∠DAB=90°,AB=CD,DO2=BO2,根据平行线分线段成比例定理得到BP2=AP2,于是得到垂足P2就是AB的二等分点,根据相似三角形的性质得到$\frac{B{O}_{3}}{D{O}_{3}}$=$\frac{B{P}_{2}}{CD}$=$\frac{1}{2}$,根据平行线分线段成比例定理得到AP3=2BP3,于是得到垂足P3就是AB的三等分点;于是得到结论.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠DAB=90°,AB=CD,DO2=BO2,
∵O2P2⊥AB,
∴O2P2∥AB,
∴$\frac{B{O}_{2}}{D{O}_{2}}=\frac{B{P}_{2}}{A{P}_{2}}$=1,
∴BP2=AP2,
∴垂足P2就是AB的二等分点,
∵AB∥CD,
∴△CDO3∽△BP2O3,
∴$\frac{B{O}_{3}}{D{O}_{3}}$=$\frac{B{P}_{2}}{CD}$=$\frac{1}{2}$,
∵O3P3⊥AB,
∴O3P3∥AD,
∴$\frac{B{P}_{3}}{A{P}_{3}}$=$\frac{B{O}_{3}}{D{O}_{3}}$=$\frac{1}{2}$,
∴AP3=2BP3,
∴垂足P3就是AB的三等分点;
∴再依次做下去,就得到AB的四等分点,…n等分点.
点评 本题考查了相似三角形的判定和性质,平行线分线段成比例定理.矩形的性质,正确的识别图形是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
15.130万(即1300000)这个数用科学记数法可表示为( )
| A. | 1.3×104 | B. | 1.3×105 | C. | 1.3×106 | D. | 1.3×107 |
10.已知某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )
| A. | 不盈不亏 | B. | 盈利10元 | C. | 亏损10元 | D. | 盈利50元 |
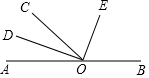 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°