题目内容
7.如图1,已知△ABC中,∠ABC=45°,点E为AC上的一点,连接BE,在BC上找一点G,使得AG=AB,AG交BE于K.(1)若∠ABE=30°,且∠EBC=∠GAC,BK=4,求AC的长度.
(2)如图2,过点A作DA⊥AE交BE于点D,过D、E分别向AB所在的直线作垂线,垂足分别为点M、N,且NE=AM,若D为BE的中点,证明:$\sqrt{5}$DG=2AG.
(3)如图3,将(2)中的条件“若D为BE的中点”改为“若点K为AG的中点”,其他条件不变,请直接写出$\frac{AE}{BC}$的值.
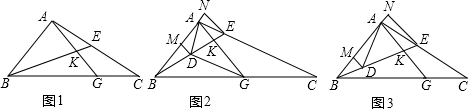
分析 (1)如图1中,作AH⊥BG于H.在Rt△ABK中,求出AK、AB,在Rt△ABH中,求出AH,在Rt△AHC中,证明∠C=30°,即可推出AC=2AH,由此解决问题.
(2)如图2中,连接EG.由△MAD≌△NEA,推出AD=AE再证明△BAD≌△GAE,推出BD=EG=DE,∠ABD=∠AGE,推出DGE是等腰直角三角形,设AD=AE=a,求出DG、AG即可解决问题.
(3)如图3中,作AH⊥BE,连接EG.由△AKH≌△GKE,推出EG=AH,HK=EK,设KH=EK=a,则AH=HE=EG=2a,BE=6a,AD=AE=2$\sqrt{2}$a,在Rt△BEG中,BG=$\sqrt{(6a)^{2}+(2a)^{2}}$=2$\sqrt{10}$a,由△ABD∽△ACG,得$\frac{BD}{GC}$=$\frac{AD}{AG}$,求出GC,即可解决问题.
解答 解:(1)如图1中,作AH⊥BG于H.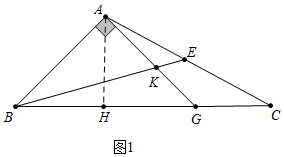
在Rt△ABK中,∵∠BAK=90°,∠ABK=30°,BK=4,
∴AK=$\frac{1}{2}$BK=2,AB=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵AB=AG,∠BAC=90°,
∴∠ABC=∠AGB=45°,∠CBE=∠CAG=15°,
∵∠AGB=∠C+∠CAG,
∴∠C=30°,
在Rt△AHC中,∵∠AHC=90°,∠C=30°,
∴AC=2AH,
在Rt△ABH中,AH=BH=$\frac{\sqrt{2}}{2}$AB=$\sqrt{6}$,
∴AC=2$\sqrt{6}$.
(2)如图2中,连接EG.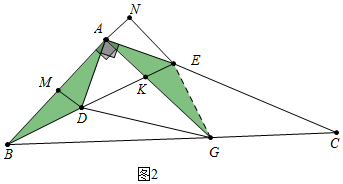
∵DM⊥AB,EN⊥BA,
∴∠AMD=∠N=∠DAE=90°,
∴∠MAD+∠NAE=90°,∠NAE+∠NEA=90°,
∴∠MAD=∠NEA,
在△MAD和△NEA中,
$\left\{\begin{array}{l}{∠MAD=∠AEN}\\{AM=NE}\\{∠AMD=∠N}\end{array}\right.$,
∴△MAD≌△NEA,
∴AD=AE,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠GAE,
在△BAD和△GAE中,
$\left\{\begin{array}{l}{BA=AG}\\{∠BAD=∠GAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△GAE,
∴BD=EG=DE,∠ABD=∠AGE,
∵∠AKB=∠EKG,
∴∠KEG=∠KAB=90°,
∴△DGE是等腰直角三角形,设AD=AE=a,
∴∠ADE=∠EDG=45°,
∴∠ADG=90°,
∴DE=BD=EG=$\sqrt{2}$a,DG=$\sqrt{2}$DE=2a,
在Rt△ADG中,AG=$\sqrt{{a}^{2}+(2a)^{2}}$=$\sqrt{5}a$,
∴$\frac{DG}{AG}$=$\frac{2a}{\sqrt{5}a}$,
∴$\sqrt{5}$DG=2AG.
(3)如图3中,作AH⊥BE,连接EG.
由(2)可知∠BEG=90°,BD=EG,
∵AH⊥BE,
∴∠AHK=∠KEG,
在△AKH和△GKE中,
$\left\{\begin{array}{l}{∠AKH=∠EKG}\\{∠AKH=∠GEK}\\{AK=KG}\end{array}\right.$,
∴△AKH≌△GKE,
∴EG=AH,HK=EK,设KH=EK=a,则AH=HE=EG=2a,BE=6a,AD=AE=2$\sqrt{2}$a,
在Rt△BEG中,BG=$\sqrt{(6a)^{2}+(2a)^{2}}$=2$\sqrt{10}$a,
∴AB=AG=2$\sqrt{5}$a,
∵∠BAD=∠GAC,∠ADB=∠AGC=135°,
∴△ABD∽△ACG,
∴$\frac{BD}{GC}$=$\frac{AD}{AG}$,
∴$\frac{2a}{GC}$=$\frac{2\sqrt{2}a}{2\sqrt{5}a}$,
∴GC=$\sqrt{10}$a,
∴BC=BG+GC=3$\sqrt{10}$a,
∴$\frac{AE}{BC}$=$\frac{2\sqrt{2}a}{3\sqrt{10}a}$=$\frac{2\sqrt{5}}{15}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的性质、勾股定理、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.

| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 6.5 | -4 | -2.5 | -2 | -2.5 | … |
| A. | 1.3×104 | B. | 1.3×105 | C. | 1.3×106 | D. | 1.3×107 |
| A. | a<2 | B. | a=2 | C. | a>2 | D. | a≤2 |
| A. | 9.4×106 | B. | 9.4×105 | C. | 0.94×106 | D. | 94×104 |
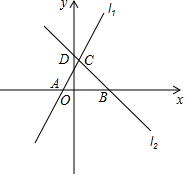 如图,直线l1,l2交于点C,直线l1与x轴交于A;直线l2与x轴交于B(3,0),与y轴交于D(0,3),已知直线l1的函数解析式为y=2x+2.
如图,直线l1,l2交于点C,直线l1与x轴交于A;直线l2与x轴交于B(3,0),与y轴交于D(0,3),已知直线l1的函数解析式为y=2x+2.