题目内容
 如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?
考点:旋转的性质
专题:
分析:(1)旋转△ADF可得△ABE,通过证明△ADF≌△ABE即可说明问题;
(2)旋转的定义和旋转角的定义解答即可;
(3)根据旋转的性质得BE=DF,∠1=∠2,再根据三角形内角定理得到∠DHB=∠BAE=90°,所以BE⊥DF.
(2)旋转的定义和旋转角的定义解答即可;
(3)根据旋转的性质得BE=DF,∠1=∠2,再根据三角形内角定理得到∠DHB=∠BAE=90°,所以BE⊥DF.
解答:解:(1)旋转△ADF可得△ABE,
理由如下:
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠DAF=90°,
在△ADF和△ABE中,
,
∴△ADF≌△ABE,
∴旋转△ADF可得△ABE;
(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90°;
(3)BE=DF且BE⊥BE.理由如下:
延长BE交F于H点,如图,
∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
∵△ABE按逆时针方向旋转90°△ADF,
∴BE=DF,∠1=∠2,
∵∠3=∠4,
∴∠DHB=∠BAE=90°,
∴BE⊥DF.
理由如下:
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠DAF=90°,
在△ADF和△ABE中,
|
∴△ADF≌△ABE,
∴旋转△ADF可得△ABE;
(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90°;
(3)BE=DF且BE⊥BE.理由如下:
延长BE交F于H点,如图,
∵四边形ABCD为正方形,

∴AD=AB,∠DAB=90°,
∵△ABE按逆时针方向旋转90°△ADF,
∴BE=DF,∠1=∠2,
∵∠3=∠4,
∴∠DHB=∠BAE=90°,
∴BE⊥DF.
点评:本题考查了正方形的性质、全等三角形的判定和性质以及旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
下列运算正确的是( )
| A、2x+3y=5xy |
| B、(-3x2y)3=-9x6y3 |
| C、x3•x4=x7 |
| D、(x-y)3=x3-y3 |
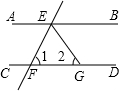 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠1=72°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠1=72°,则∠2的度数为( )| A、36° | B、54° |
| C、45° | D、68° |
 如图所示,在矩形ABCD中,AD=10,DC=8,点E为AB边上一点,△BCE沿EC所在直线翻折,使得B点刚好落在AD边上F处.
如图所示,在矩形ABCD中,AD=10,DC=8,点E为AB边上一点,△BCE沿EC所在直线翻折,使得B点刚好落在AD边上F处. △ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:AC=3AF.
△ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:AC=3AF.