题目内容
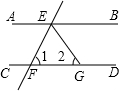如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF．若∠1=72°，则∠2的度数为（ ）| A、36° | B、54° |
| C、45° | D、68° |
考点：平行线的性质
专题：
分析：两直线平行，同旁内角互补，可求出∠FEB，再根据角平分线的性质，可得到∠BEG，然后用两直线平行，内错角相等求出∠2．
解答：解：如图，∵AB∥CD，
∴∠BEF=180°-∠1=180°-72°=108°，∠2=∠BEG，
又∵EG平分∠BEF，
∴∠BEG=
∠BEF=
×108°=54°，
∴∠2=∠BEG=54°．
故选：B．
∴∠BEF=180°-∠1=180°-72°=108°，∠2=∠BEG，
又∵EG平分∠BEF，
∴∠BEG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠2=∠BEG=54°．
故选：B．
点评：本题应用的知识点为：两直线平行，内错角相等；同旁内角互补．
练习册系列答案
天天练口算系列答案
相关题目
如图，直线AB、CD、EF相交于点O，则∠AOC的对顶角是平面上有5个点，其中仅有3点在同一直线上，过每2点作一条直线，一共可以作直线（ ）条．
| A、7 | B、6 | C、9 | D、8 |
如图，AB∥EF，∠C=90°，则α、β和γ的关系是（ ）| A、β=α+γ |
| B、α+β+γ=180° |
| C、α+β-γ=90° |
| D、β+γ-α=180° |
如图，正方形ABCD的边长为2，点E是BC边上一点，EF⊥AE交CD于点F，设BE=x，CF=y，则下列表示y关于x的函数图象中正确的是（ ）
下列二次根式中，能与
合并的是（ ）
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
园丁住宅小区有一块草坪如图所示，已知AB=1.5米，BC=2米，DA=6.5米，DC=6米，且AB⊥BC，这块草坪的面积是（ ）| A、24米2 |
| B、36米2 |
| C、18米2 |
| D、9米2 |
如图，四边形ABCD是正方形，E是AD上任意一点，延长BA到F，使得AF=AE，连接DF：
如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．