题目内容
在△ABC中,CD⊥AB于D,且∠A=45°,∠B=30°,AC=5.则BD的长为 .
考点:勾股定理
专题:
分析:作出图形,判断出△ACD是等腰直角三角形,然后求出CD,再根据直角三角形30°角所对的直角边等于斜边的一半求出BC=2CD,然后利用勾股定理列式计算即可得解.
解答: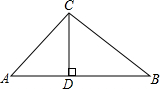 解:如图,∵CD⊥AB于D,∠A=45°,
解:如图,∵CD⊥AB于D,∠A=45°,
∴△ACD是等腰直角三角形,
∴CD=
AC=
×5=
,
∵∠B=30°,
∴BC=2CD=2×
=5
,
在Rt△BCD中,BD=
=
.
故答案为:
.
 解:如图,∵CD⊥AB于D,∠A=45°,
解:如图,∵CD⊥AB于D,∠A=45°,∴△ACD是等腰直角三角形,
∴CD=
| ||
| 2 |
| ||
| 2 |
5
| ||
| 2 |
∵∠B=30°,
∴BC=2CD=2×
5
| ||
| 2 |
| 2 |
在Rt△BCD中,BD=
(5
|
5
| ||
| 2 |
故答案为:
5
| ||
| 2 |
点评:本题考查了勾股定理,等腰直角三角形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质与定理是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 如图,在正方形ABCD中,点E在CD上,CE=
如图,在正方形ABCD中,点E在CD上,CE= 如图,BC是⊙O的直径,点A是
如图,BC是⊙O的直径,点A是