题目内容
已知,平面直角坐标系中,矩形OABC的边OC在x轴正半轴上,边OA在y轴正半轴上,B点的坐标为(4,3).将△AOC沿对角线AC所在的直线翻折,得到△AO′C,点O′为点O的对称点,CO′与AB相交于点E(如图①).
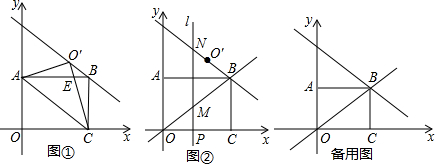
(1)试说明:EA=EC;
(2)求直线BO′的解析式;
(3)作直线OB(如图②),直线l平行于y轴,分别交x轴、直线OB、O′B于点P、M、N,设P点的横坐标为m(m>0),y轴上是否存在点F,使得△FMN为等腰直角三角形?若存在,请求出此时m的值;若不存在,请说明理由.

(1)试说明:EA=EC;
(2)求直线BO′的解析式;
(3)作直线OB(如图②),直线l平行于y轴,分别交x轴、直线OB、O′B于点P、M、N,设P点的横坐标为m(m>0),y轴上是否存在点F,使得△FMN为等腰直角三角形?若存在,请求出此时m的值;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)由折叠和矩形的性质可证明∠BAC=∠ECA,可得EA=EC;
(2)设BO′交y轴于点D,由题意可知O′、B到AC的距离相等,可知BO′∥AC,可证得BC=AD,可求得D点坐标,且过B,利用待定系数法可求得直线BO′的解析式;
(3)分别利用m表示出M、N的坐标,可表示出MN,分∠FMN、∠FNM和∠MFN为直角三种情况,分别求得F点的坐标,表示出FM、FN,分别得到关于m的方程可求得m.
(2)设BO′交y轴于点D,由题意可知O′、B到AC的距离相等,可知BO′∥AC,可证得BC=AD,可求得D点坐标,且过B,利用待定系数法可求得直线BO′的解析式;
(3)分别利用m表示出M、N的坐标,可表示出MN,分∠FMN、∠FNM和∠MFN为直角三种情况,分别求得F点的坐标,表示出FM、FN,分别得到关于m的方程可求得m.
解答:解:
(1)∵四边形OABC为矩形,
∴AB∥OC,
∴∠BAC=∠ACO,
又△AOC沿对角线AC所在的直线翻折,得到△AO′C,
∴∠ACO=∠ECA,
∴∠EAC=∠ECA,
∴EA=EC;
(2)如图,设BO′交y轴于点D,由题意可知S△ABC=S△AOC=S△ACO′,且同底,
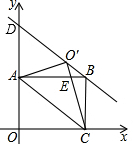
∴O′、B到AC的距离相等,
∴BO′∥AC,且BC∥AO,
∴四边形ACBD为平行四边形,
∴AD=BC=3,且OA=3,
∴D点坐标为(0,6),又直线BO′过点B,
设直线BO′解析式为y=kx+6,把B点坐标代入可求得k=-
,
∴直线BO′的解析式为:y=-
x+6①;
(3)∵B为(4,3),
∴直线BO为y=
x②,∵l∥y轴,交x轴于P,P点的横坐标为m,
∴P(m,0)(m>0),
∴直线l的解析式为x=m③,
解②③得M(m,
m);解①②得:N(m,-
m+6),
∴MN=|-
m+6|,
Ⅰ)当∠FMN=90°且△FMN为等腰三角形时,F(0,
m),
∴FM=MN,即:m=|-
m+6|,
解得:m=
或m=12,
Ⅱ)同理当∠FNM=90°且△FMN为等腰三角形时,F(0,-
m+6),
∴FN=MN,即:m=|-
m+6|,
解得:m=
或m=12,
Ⅲ)当∠MFN=90°且△FMN为等腰三角形时,F(0,3),
∴FM2=m2+(
m-3)2,
FN2=m2+(
m-3)2,
MN2=(-
m+6)2,
∴MN2=FM2+FN2,
∴m2+(
m-3)2+m2+(
m-3)2=(-
m+6)2,整理可得
m2+18m-18=0,解得m=
或m=-12(舍去);
综上可知存在使得△FMN为等腰直角三角形的点F,此时m的值为
或
或12.
(1)∵四边形OABC为矩形,
∴AB∥OC,
∴∠BAC=∠ACO,
又△AOC沿对角线AC所在的直线翻折,得到△AO′C,
∴∠ACO=∠ECA,
∴∠EAC=∠ECA,
∴EA=EC;
(2)如图,设BO′交y轴于点D,由题意可知S△ABC=S△AOC=S△ACO′,且同底,

∴O′、B到AC的距离相等,
∴BO′∥AC,且BC∥AO,
∴四边形ACBD为平行四边形,
∴AD=BC=3,且OA=3,
∴D点坐标为(0,6),又直线BO′过点B,
设直线BO′解析式为y=kx+6,把B点坐标代入可求得k=-
| 3 |
| 4 |
∴直线BO′的解析式为:y=-
| 3 |
| 4 |
(3)∵B为(4,3),
∴直线BO为y=
| 3 |
| 4 |
∴P(m,0)(m>0),
∴直线l的解析式为x=m③,
解②③得M(m,
| 3 |
| 4 |
| 3 |
| 4 |
∴MN=|-
| 3 |
| 2 |
Ⅰ)当∠FMN=90°且△FMN为等腰三角形时,F(0,
| 3 |
| 4 |
∴FM=MN,即:m=|-
| 3 |
| 2 |
解得:m=
| 12 |
| 5 |
Ⅱ)同理当∠FNM=90°且△FMN为等腰三角形时,F(0,-
| 3 |
| 4 |
∴FN=MN,即:m=|-
| 3 |
| 2 |
解得:m=
| 12 |
| 5 |
Ⅲ)当∠MFN=90°且△FMN为等腰三角形时,F(0,3),
∴FM2=m2+(
| 3 |
| 4 |
FN2=m2+(
| 3 |
| 4 |
MN2=(-
| 3 |
| 2 |
∴MN2=FM2+FN2,
∴m2+(
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 7 |
| 8 |
| 12 |
| 7 |
综上可知存在使得△FMN为等腰直角三角形的点F,此时m的值为
| 12 |
| 5 |
| 12 |
| 7 |
点评:本题主要考查待定系数法求函数解析式和等腰三角形的判定、折叠的性质、勾股定理等知识点的综合应用.掌握折叠的性质及等腰三角形的判定和性质是解题的关键,在(2)中判断出BO′∥AC是解题的关键,在(3)中利用m表示出FN、FM和MN得到关于m的方程是解题的关键,注意分类讨论思想和方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
John于早上6点x分钟从A地出发,在当天早上6点y分钟抵达B地.他发现,在这段行程的起点和终点时刻,时针和分针所成的夹角都是110°,那么John从A至B地耗时( )
| A、35分钟 | B、38分钟 |
| C、40分钟 | D、44分钟 |
 如图,已知,∠B=∠C=90°,点E是BC边上的中点,DE平分∠ADC,结论:①AE平分∠DAB;②AE⊥DE;③AE=DE;④S梯形ABCD=
如图,已知,∠B=∠C=90°,点E是BC边上的中点,DE平分∠ADC,结论:①AE平分∠DAB;②AE⊥DE;③AE=DE;④S梯形ABCD=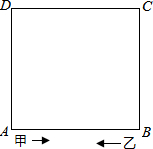 如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米,
如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米,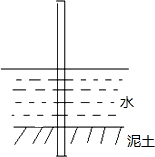 一根竹竿插入一水池底部的淤泥中(如图),竹竿的入泥部分占全长的
一根竹竿插入一水池底部的淤泥中(如图),竹竿的入泥部分占全长的