题目内容
已知多项式A=2x+4y-5,B=2(x+y)-(x+3).
(1)当x=y=-5时,求A-B的值;
(2)A-2B的值与x、y的取值是否有关?试说明理由.
(1)当x=y=-5时,求A-B的值;
(2)A-2B的值与x、y的取值是否有关?试说明理由.
考点:整式的加减—化简求值
专题:
分析:(1)根据整式的加减,可化简整式,根据代数式求值,可得答案;
(2)根据整式加减,可得答案.
(2)根据整式加减,可得答案.
解答:解:(1)A-B=(2x+4y-5)-[2(x+y)-(x+3)]
=2x+4y-5-[2x+2y-x-3]
=2x+4y-5-2x-2y+x+3
=x+2y-2,
当x=y=-5时,原式=-5+2×(-5)-2=-5-10-2=-17;
(2)A-2B的值与x、y的取值无关,理由如下:
A-2B=(2x+4y-5)-2[2(x+y)-(x+3)]
=2x+4y-5-2[2x+2y-x-3]
=2x+4y-5-4x-4y+2x+3
(2x-4x+2x)+(4y-4y)+(-5+3)
=-2.
=2x+4y-5-[2x+2y-x-3]
=2x+4y-5-2x-2y+x+3
=x+2y-2,
当x=y=-5时,原式=-5+2×(-5)-2=-5-10-2=-17;
(2)A-2B的值与x、y的取值无关,理由如下:
A-2B=(2x+4y-5)-2[2(x+y)-(x+3)]
=2x+4y-5-2[2x+2y-x-3]
=2x+4y-5-4x-4y+2x+3
(2x-4x+2x)+(4y-4y)+(-5+3)
=-2.
点评:本题考查了整式的化简求值,注意多项式加减多项式时要加括号.

练习册系列答案
相关题目
John于早上6点x分钟从A地出发,在当天早上6点y分钟抵达B地.他发现,在这段行程的起点和终点时刻,时针和分针所成的夹角都是110°,那么John从A至B地耗时( )
| A、35分钟 | B、38分钟 |
| C、40分钟 | D、44分钟 |
一个整式减去3m,结果等于5m2-3m-5.这个整式是( )
| A、5m2-5 |
| B、5m2-6m-5 |
| C、5m2+5 |
| D、-5m-6m+5 |
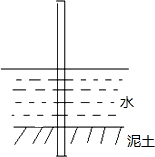 一根竹竿插入一水池底部的淤泥中(如图),竹竿的入泥部分占全长的
一根竹竿插入一水池底部的淤泥中(如图),竹竿的入泥部分占全长的