题目内容
若x2-
x+k=(x-a)2成立,则ak= .
| 1 |
| 2 |
考点:配方法的应用
专题:计算题
分析:已知等式右边利用完全平方公式化简,利用多项式相等的条件求出a与k的值,即可确定出ak的值.
解答:解:x2-
x+k=(x-a)2=x2-2ax+a2,
可得-
=-2a,a2=k,
解得:a=
,k=
,
则ak=
,
故答案为:
.
| 1 |
| 2 |
可得-
| 1 |
| 2 |
解得:a=
| 1 |
| 4 |
| 1 |
| 16 |
则ak=
| 1 |
| 64 |
故答案为:
| 1 |
| 64 |
点评:此题考查了配方法的应用,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
一个整式减去3m,结果等于5m2-3m-5.这个整式是( )
| A、5m2-5 |
| B、5m2-6m-5 |
| C、5m2+5 |
| D、-5m-6m+5 |
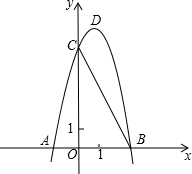 如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求
如图,抛物线y=ax2+bx+8与x轴交于点A(-2,0)、点B,与y轴交于点C,顶点为D,OC=2OB,求