题目内容
5.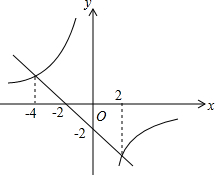 若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )
若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )| A. | 0<x≤2或x≤-4 | B. | -4≤x<0或x≥2 | C. | $-2\sqrt{2}$≤x<0或x$≥2\sqrt{2}$ | D. | x$≤-2\sqrt{2}$或0$<x≤2\sqrt{2}$ |
分析 根据图形找出点的坐标,利用待定系数法求出一次函数和反比例函数解析式,将一次函数图象向上移2个单位长度找出新的一次函数解析式,联立新一次函数解析式和反比例函数解析式成方程组,通过解方程组求出交点坐标,结合函数图象即可得出不等式的解集.
解答 解:将(-2,0)、(0,-2)代入y=kx+b,
$\left\{\begin{array}{l}{-2k+b=0}\\{b=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
∴一次函数解析式为y=-x-2.
当x=2时,y=-x-2=-4,
∴一次函数图象与反比例函数图象的一个交点坐标为(2,-4),
∴k=2×(-4)=-8,
∴反比例函数解析式为y=-$\frac{8}{x}$.
将一次函数图象向上移2个单位长度得出的新的函数解析式为y=-x.
联立新一次函数及反比例函数解析式成方程组,
$\left\{\begin{array}{l}{y=-x}\\{y=-\frac{8}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-2\sqrt{2}}\\{{y}_{1}=-2\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2\sqrt{2}}\\{{y}_{2}=2\sqrt{2}}\end{array}\right.$.
观察函数图象可知:当-2$\sqrt{2}$<x<0或x>2$\sqrt{2}$时,新一次函数图象在反比例函数图象下方,
∴不等式-x≤-$\frac{8}{x}$的解集为-2$\sqrt{2}$≤x<0或x≥2$\sqrt{2}$.
故选C.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求一次(反比例)函数解析式以及一次函数图象与几何变换,根据图形中点的坐标利用待定系数法求出一次(反比例)函数解析式是解题的关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案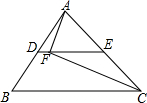 如图,在△ABC中,D,E分别是AB,AC的中点,AC=20,F是DE上一点,连接AF,CF,DF=4.若∠AFC=90°,则BC的长度为( )
如图,在△ABC中,D,E分别是AB,AC的中点,AC=20,F是DE上一点,连接AF,CF,DF=4.若∠AFC=90°,则BC的长度为( )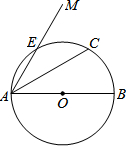 如图,AB是⊙O的直径,射线AM经过⊙O上的点E,弦AC平分∠MAB,过点C作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,射线AM经过⊙O上的点E,弦AC平分∠MAB,过点C作CD⊥AM,垂足为D. 如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.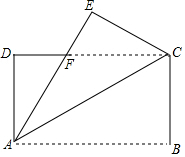 如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.
如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.