题目内容
16.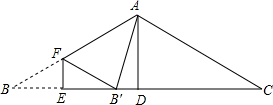 如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.
如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.
分析 由等腰三角形的性质可知∠AFB=60°,∠FAB′<60°,所以当△AB′F为直角三角形时,只有∠FB′A=90°,设BE=x,则B′D=3-2x,易证△FEB′∽△B′DA,由相似三角形的性质:对应边的比值相等可建立关于x的方程,解方程求出x的值即可.
解答  解:∵AB=AC,∠BAC=120°,AD⊥BC,垂足为D.
解:∵AB=AC,∠BAC=120°,AD⊥BC,垂足为D.
∴∠B=30°,BD=CD=$\frac{1}{2}$BC=3,
∵把∠B沿EF折叠,使点B落在点B′处.
∴∠FB′B=30°,
∴∠AFB=60°,∠FAB′<60°,
∴当△AB′F为直角三角形时,只有∠FB′A=90°,
设BE=x,则B′D=3-2x,
∵∠FEB′=∠ADB′=90°,∠EFB′=∠AB′D,
∴△FEB′∽△B′DA,
∴EF:B′D=EB′:AD,
∵∠B=30°,BE=x,BD=3,
∴EF=$\frac{\sqrt{3}}{3}$x,AD=$\sqrt{3}$
∴$\frac{\sqrt{3}}{3}$x:(3-2x)=x:$\sqrt{3}$,
解得:x=1,
∴BE=1,
故答案为:1.
点评 本题考查了折叠的性质,用到的知识点有等腰三角形的性质、勾股定理的运用、特殊角的锐角三角形函数值以及相似三角形的判定和性质,题目的综合性较强,难度中等,解题的关键是能够证明△FEB′∽△B′DA,再利用相似三角形的性质解答,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.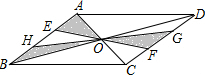 如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
 如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
8.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为2a,则纸片的剩余部分的面积为 ( )
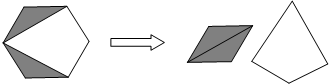

| A. | 5a | B. | 4a | C. | 3a | D. | 2a |
 如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.
如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.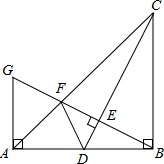 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G.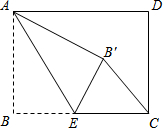 如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=4,点E是BC边上一点,连接AE,△ABE沿AE折叠,使点B落到点B′处,连接B′C,若B′C∥AE,则B′C的值为2.
如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=4,点E是BC边上一点,连接AE,△ABE沿AE折叠,使点B落到点B′处,连接B′C,若B′C∥AE,则B′C的值为2.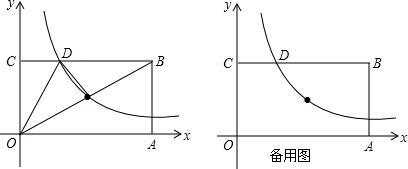
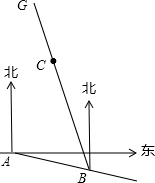 如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.
如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.